Questions and Problems
- I wish I had an answer for that, because I’m getting tired of answering that question.
- —Yogi Berra, New York Yankees Sports Illustrated, June 11, 1984
The subscript to each of the problem numbers indicates the level of difficulty, i.e., A, least difficult; B, moderate difficulty; C, fairly difficult; D, (double black diamond), most difficult.  For example, P1-5B means “1” is the Chapter number, “5” is the problem number, “B” is the problem difficulty, in this case B means moderate difficulty.
For example, P1-5B means “1” is the Chapter number, “5” is the problem number, “B” is the problem difficulty, in this case B means moderate difficulty.
Before solving the problems, state or sketch qualitatively the expected results or trends.
Questions
Q1-1A Read through the Preface. Write a paragraph describing both the content goals and the intellectual goals of the course and text. Also describe what’s on the Web site and how the Web site can be used with the text and course.
Q1-2A View the photos and schematics on the Web site under Essentials of Chemical Reaction Engineering—Chapter 1. Look at the QuickTime videos. Write a paragraph describing two or more of the reactors. What similarities and differences do you observe between the reactors on the Web (e.g., www.loebequipment.com), on the Web site, and in the text? How do the used reactor prices compare with those in Table 1-1?
Q1-3A Surf the Web and the CRE Web site (www.umich.edu/~elements/5e/index.html). Go on a scavenger hunt using the summary notes for Chapter 1 on the Web site. Take a quick look at the Web Modules and list the ones that you feel are the most novel applications of CRE.
Q1-4A What does a negative number for the rate of formation of species (e.g., species A), rA = –3mol/dm3·s, signify? What does a positive number signify? Explain.
Q1-5A What assumptions were made in the derivation of the design equation for:
- The batch reactor (BR)?
- The CSTR?
- The plug-flow reactor (PFR)?
- The packed-bed reactor (PBR)?
- State in words the meanings of –rA and –
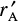 .
.
Q1-6A Use the mole balance to derive an equation analogous to Equation (1-7) for a fluidized CSTR containing catalyst particles in terms of the catalyst weight, W, and other appropriate terms.
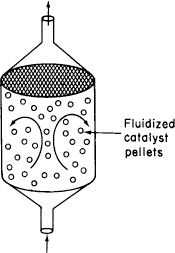
Figure Q1-6 Fluidized Bed CSTR.
Equation Q1-6
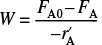
Problems
Pl–1A
- Revisit Example 1-1. Rework this example using Equation (3-1) on page 71.
- Revisit Example 1-2. Calculate the volume of a CSTR for the conditions used to calculate the plug-flow reactor volume in Example 1-2. Which volume is larger, the PFR or the CSTR? Explain why. Suggest two ways to work this problem incorrectly.
- Revisit Example 1-2. Calculate the time to reduce the number of moles of A to 1% of its initial value in a constant-volume batch reactor for the same reaction and data in Example 1-2. Suggest two ways to work this problem incorrectly.
Pl-2A
Find the Interactive Computer Games (ICG) on the CRE Web site. Play this game and then record your performance number, which indicates your mastery of the material.
ICG Kinetics Challenge 1 Performance # _____________________
P1-3A
The reaction

takes place in an unsteady CSTR. The feed is only A and B in equimolar proportions. Which of the following sets of equations gives the correct set of mole balances on A, B, and C? Species A and B are disappearing and species C is being formed. Circle the correct answer where all the mole balances are correct.
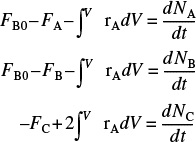
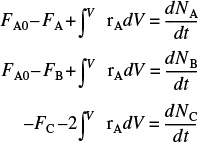
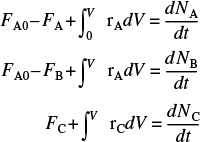
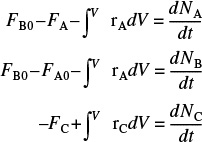
- None of the above.
P1-4B
Schematic diagrams of the Los Angeles basin are shown in Figure P1-4B. The basin floor covers approximately 700 square miles (2×1010 ft2) and is almost completely surrounded by mountain ranges. If one assumes an inversion height in the basin of 2,000 ft, the corresponding volume of air in the basin is 4×1013 ft3. We shall use this system volume to model the accumulation and depletion of air pollutants. As a very rough first approximation, we shall treat the Los Angeles basin as a well-mixed container (analogous to a CSTR) in which there are no spatial variations in pollutant concentrations.

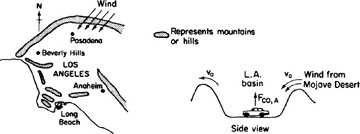
Figure P1-4B Schematic diagrams of the Los Angeles basin.
We shall perform an unsteady-state mole balance (Equation (1-4)) on CO as it is depleted from the basin area by a Santa Ana wind. Santa Ana winds are high-velocity winds that originate in the Mojave Desert just to the northeast of Los Angeles. Load the Smog in Los Angeles Basin Web Module. Use the data in the module to work parts 1-12 (a) through (h) given in the module. Load the Living Example Polymath code and explore the problem. For part (i), vary the parameters υ0, a, and b, and write a paragraph describing what you find.
There is heavier traffic in the L.A. basin in the mornings and in the evenings as workers go to and from work in downtown L.A. Consequently, the flow of CO into the L.A. basin might be better represented by the sine function over a 24-hour period.
P1-5B
The reaction

is to be carried out isothermally in a continuous-flow reactor. The entering volumetric flow rate υ0 is 10 dm3/h. (Note: FA = CAυ. For a constant volumetric flow rate υ = υ0, then FA = CAυ0. Also, CA0 = FA0/υ0 = ([5 mol/h]/[10 dm3/h]) 0.5 mol/dm3.)
Calculate both the CSTR and PFR reactor volumes necessary to consume 99% of A (i.e., CA = 0.01CA0) when the entering molar flow rate is 5 mol/h, assuming the reaction rate –rA is
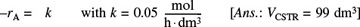
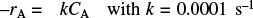
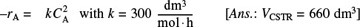
- Repeat (a), (b), and/or (c) to calculate the time necessary to consume 99.9% of species A in a 1000 dm3 constant-volume batch reactor with CA0 = 0.5 mol/dm3.
P1-6B
This problem focuses on using Polymath, an ordinary differential equation (ODE) solver, and also a nonlinear equation (NLE) solver. These equation solvers will be used extensively in later chapters. Information on how to obtain and load the Polymath Software is given in Appendix D and on the CRE Web site.
There are initially 500 rabbits (x) and 200 foxes (y) on Farmer Oat’s property near Riça, Jofostan. Use Polymath or MATLAB to plot the concentration of foxes and rabbits as a function of time for a period of up to 500 days. The predator-prey relationships are given by the following set of coupled ordinary differential equations:
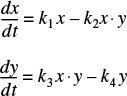

Constant for growth of rabbits k1 = 0.02 day–1
Constant for death of rabbits k2 = 0.00004/(day × no. of foxes)
Constant for growth of foxes after eating rabbits k3 = 0.0004/(day × no. of rabbits)
Constant for death of foxes k4 = 0.04 day–1
What do your results look like for the case of k3 = 0.00004/(day × no. of rabbits) and tfinal = 800 days? Also, plot the number of foxes versus the number of rabbits. Explain why the curves look the way they do.
Use Polymath or MATLAB to solve the following set of nonlinear algebraic equations
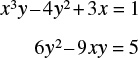
with inital guesses of x = 2, y = 2. Try to become familiar with the edit keys in Polymath and MATLAB. See the CRE Web site for instructions
Screen shots on how to run Polymath are shown at the end of Summary Notes for Chapter 1 or on the CRE Web site, www.umich.edu/~elements/5e/software/polymath-tutorial.html.
P1-7A
Enrico Fermi (1901-1954) Problems (EFP). Enrico Fermi was an Italian physicist who received the Nobel Prize for his work on nuclear processes. Fermi was famous for his “Back of the Envelope Order of Magnitude Calculation” to obtain an estimate of the answer through logic and then to make reasonable assumptions. He used a process to set bounds on the answer by saying it is probably larger than one number and smaller than another, and arrived at an answer that was within a factor of 10. See http://mathforum.org/workshops/sum96/interdisc/sheila2.html.
Enrico Fermi Problem
(a) EFP #1. How many piano tuners are there in the city of Chicago? Show the steps in your reasoning.
- Population of Chicago ___________
- Number of people per household ___________
Etc. ___________
An answer is given on the CRE Web site under Summary Notes for Chapter 1.
- EFP #2. How many square meters of pizza were eaten by an undergraduate student body population of 20,000 during the Fall term 2016?
- EFP #3. How many bathtubs of water will the average person drink in a lifetime?
P1-8A
What is wrong with this solution? The irreversible liquid phase second order reaction (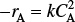 )
)
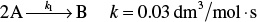
is carried out in a CSTR. The entering concentration of A, CA0, is 2 molar. And the exit concentration of A, CA is 0.1 molar. The volumetric flow rate, υ0, is constant at 3 dm3/s. What is the corresponding reactor volume?
Solution
Mole Balance
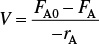
Rate Law (2nd order)
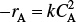
Combine
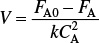
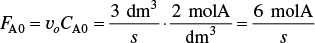
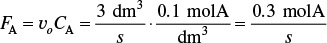
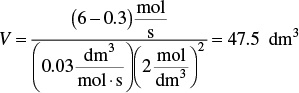
For more puzzles on what’s wrong with this solution, see additional material for each chapter on the CRE Web site home page, under “Expanded Material.”