- Random Numbers and Probability Distributions
- Casino Royale: Roll the Dice
- Normal Distribution
- The Student Who Taught Everyone Else
- Statistical Distributions in Action
- Hypothetically Yours
- The Mean and Kind Differences
- Worked-Out Examples of Hypothesis Testing
- Exercises for Comparison of Means
- Regression for Hypothesis Testing
- Analysis of Variance
- Significantly Correlated
- Summary
This chapter is from the book
This chapter is from the book
This chapter is from the book
Casino Royale: Roll the Dice
I illustrate the probability function of a discrete variable using the example of rolling two fair dice. A die has six faces, so rolling two dice can assume one of the 36 discrete outcomes, because each die can assume one of the six outcomes in a roll. Hence rolling two dice together will return one out of 36 outcomes. Also, note that if one (1) comes up on each die, the outcome will be 1 + 1 = 2, and the probability associated with this outcome is one out of thirty-six (1/36) because no other combination of the two dice will return two (2). On the other hand, I can obtain three (3) with the roll of two dice by having either of the two dice assume one and the other assuming two and vice versa. Thus, the probability of an outcome of three with a roll of two dice is 2 out of 36 (2/36).
The 36 possible outcomes obtained from rolling two dice are illustrated in Figure 6.2.
)
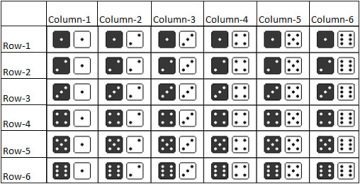
Figure 6.2 All possible outcomes of rolling two dice
Based on the possible outcomes of rolling two dice, I can generate the probability density function. I present the outcomes and the respective probabilities in the Probability column in Table 6.1.
Table 6.1 Probability Calculations for Rolling Two Dice
Sum of Two Dice, x |
f(x) |
Probability |
F(x) |
Prob <=x |
Prob > x |
2 |
1/36 |
0.028 |
1/36 |
0.028 |
0.972 |
3 |
2/36 |
0.056 |
3/36 |
0.083 |
0.917 |
4 |
3/36 |
0.083 |
6/36 |
0.167 |
0.833 |
5 |
4/36 |
0.111 |
10/36 |
0.278 |
0.722 |
6 |
5/36 |
0.139 |
15/36 |
0.417 |
0.583 |
7 |
6/36 |
0.167 |
21/36 |
0.583 |
0.417 |
8 |
5/36 |
0.139 |
26/36 |
0.722 |
0.278 |
9 |
4/36 |
0.111 |
30/36 |
0.833 |
0.167 |
10 |
3/36 |
0.083 |
33/36 |
0.917 |
0.083 |
11 |
2/36 |
0.056 |
35/36 |
0.972 |
0.028 |
12 |
1/36 |
0.028 |
1 |
1 |
0 |
The cumulative probability function F(x) specifies the probability that the random variable will be less than or equal to some value x. For the two dice example, the probability of obtaining five with a roll of two dice is 4/36. Similarly, the cumulative probability of 10/36 is the probability that the random variable will be either five or less (Table 6.1).
Figure 6.3 offers a vivid depiction of probability density functions. Remember that the probability to obtain a certain value for rolling two dice is the ratio of the number of ways that particular value can be obtained and the total number of possible outcomes for rolling two dice (36). The highest probable outcome of rolling two dice is 7, which is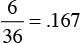 
)
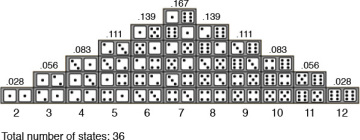
Figure 6.3 Histogram of the outcomes of rolling two dice
Source: http://hyperphysics.phy-astr.gsu.edu/hbase/math/dice.html
I have plotted the probability density function and the cumulative distribution function of the discrete random variable representing the roll of two dice in Figure 6.4 and Figure 6.5. Notice again that the probability of obtaining seven as the sum of rolling two dice is the highest and the probability of obtaining 2 or 12 are the lowest. Probability density function is a continuous function that describes the probability of outcomes for the random variable X. A histogram of a random variable approximates the shape of the underlying density function.
)
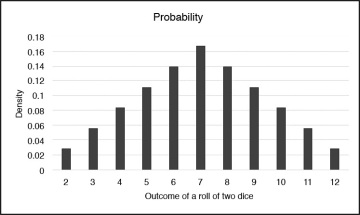
Figure 6.4 Histogram of the outcomes for rolling two dice
)
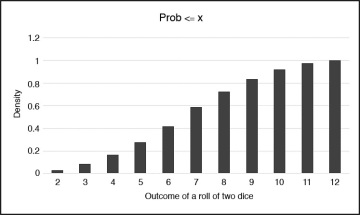
Figure 6.5 Probability distribution function for rolling two dice
Figure 6.5 depicts an important concept that I will rely on this chapter. The figure shows the probability of finding a particular value or less from rolling two dice, also known as the cumulative distribution function. For instance, the probability of obtaining four (4) or less from rolling two dice is 0.167. Stated otherwise, the probability of obtaining a value greater than four (4) from rolling two dice is 0.833.
Recall Figure 6.1, which depicted the histogram of the daily returns for Apple stock. The shape of the histogram approximated the shape of underlying density function.
){kind=link}