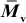This chapter is from the book
This chapter is from the book
This chapter is from the book
Problems
1.1 A polymer sample combines five different molecular-weight fractions of equal weight. The molecular weights of these fractions increase from 20,000 to 100,000 in increments of 20,000. Calculate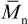 
, 
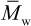, and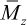 
Based upon these results, comment on whether this sample has a broad or narrow molecular-weight distribution compared to typical commercial polymer samples.
1.2 A 50-g polymer sample was fractionated into six samples of different weights given in the table below. The viscosity-average molecular weight,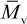 
, of each was determined and is included in the table. Estimate the number-average and weight-average molecular weights of the original sample. For these calculations, assume that the molecular-weight distribution of each fraction is extremely narrow and can be considered to be monodisperse. Would you classify the molecular-weight distribution of the original sample as narrow or broad?
Fraction |
Weight (g) |
|
1 |
1.0 |
1500 |
2 |
5.0 |
35,000 |
3 |
21.0 |
75,000 |
4 |
15.0 |
150,000 |
5 |
6.5 |
400,000 |
6 |
1.5 |
850,000 |
1.3 The Schultz–Zimm 11 molecular-weight-distribution function can be written as
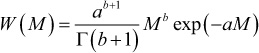
where a and b are adjustable parameters (b is a positive real number) and Γ is the gamma function (see Appendix E) that is used to normalize the weight fraction.
(a) Using this relationship, obtain expressions for 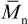and 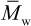in terms of a and b and an expression for Mmax, the molecular weight at the peak of the W(M) curve, in terms of .
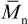(b) Derive an expression for Mmax, the molecular weight at the peak of the W(M) curve, in terms of .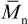
(c) Show how the value of b affects the molecular-weight distribution by graphing W(M) versus M on the same plot for b = 0.1, 1, and 10 given that 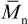= 10,000 for the three distributions.
Hint: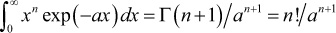 
(if n is a positive integer).
1.4 The following requested calculations refer to Examples 1.1, 1.2, and 1.3 in the text:
(a) Calculate the z-average molecular weight, 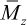, of the discrete molecular weight distribution described in Example 1.1.
(b) Calculate the z-average molecular weight, 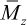, of the continuous molecular-weight distribution shown in Example 1.2.
(c) Obtain an expression for the z-average degree of polymerization,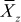 
, for the Flory distribution described in Example 1.3.