- Defining Operations Management
- Organizational Decision Levels
- Key Terminology
- Critical Processes
- Measuring Productivity Levels
- Inventory Determination
- Inventory Policy Choices
- Inventory Policy in a Fixed-Order Quantity System
- Independent Versus Dependent Demand
- ABC Inventory Classification
- Vendor Managed Inventory (VMI)
- Challenges Facing the Modern Operations Manager
- Discussion Questions
Inventory Policy Choices
As discussed earlier an organization’s inventory policy must answer the two basic questions: when to order and how much to order. There are two basic categories or choices in inventory policy that accomplish this: fixed-order quantity systems and fixed-time period systems. They work in slightly different ways. Let’s look at these now.
Fixed-Order Quantity System
The first policy choice is through a system called a fixed-order quantity system. Therefore, two variables define this system and answer the two basic questions of when to order and how much. The first is an order quantity, Q, and the second is a reorder point, ROP. As the name suggests, the quantity ordered with this system is constant or fixed and is denoted by Q. An order is placed when the inventory position drops to some predetermined level. This predetermined level is called the reorder point and is usually noted as ROP. Together these variables specify when to place an order: when inventory reaches the ROP. They also specify how much to order: the quantity Q.
A graphical presentation of this model is shown in Figure 1-5. Notice that the system assumes a constant demand rate of d by which the inventory position (IP) is reduced. When the IP reaches the ROP, an order is placed for the quantity Q. When goods arrive, the inventory is replenished, and all at once the inventory position is increased by Q. However, inventory cannot arrive the moment an order is placed as there is a certain amount of lead time, L, during which we have to wait for the order.
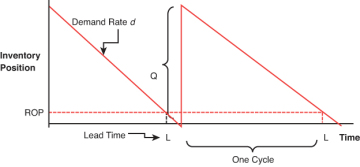
Figure 1-5 Fixed-order quantity systemt
Here inventory is monitored on a continual basis, and the assumption is that we always know the current level of inventory. When inventory levels reach the ROP, an order of quantity Q is placed. For example, let’s assume that a grocer uses a fixed-order quantity system for its inventory of canned tomato soup. Its policy may be that it always orders 200 cans of soup, for which it gets a nice quantity discount, and the order is made when the number of cans of soup drops to 25. Therefore, the ROP = 25, and the Q = 200.
In the classic version of this system Q is computed as the economic order quantity (EOQ)—an economically optimal order quantity—which we will compute later. For this reason this system is sometimes called the economic order quantity (EOQ) model. Other terms used to describe it are the Q-model as the quantity Q is constant. Sometimes it is called a continuous review system, as the inventory levels are continuously monitored. The model has even been called a sawtooth model, as the graph of inventory looks like a sawtooth. All these terms refer to the same type of inventory system, describing different features of the system itself.
Fixed-Time Period System
The second inventory policy is determined by a system called a fixed-time period system shown in Figure 1-6. This system checks inventory levels in fixed time intervals labeled as T. The result is that the quantity ordered varies based upon the inventory position when the system is checked. The system sets a target inventory level it wants to maintain, say R. Inventory is checked every T intervals, say every week or every two weeks, and an order is placed to restore the inventory level back to R. Based on the inventory level at time period T, the amount of inventory that needs to be ordered will be some quantity Q that varies from period to period. This quantity Q is the difference between the target inventory R and how much inventory is in stock—the IP at time T:
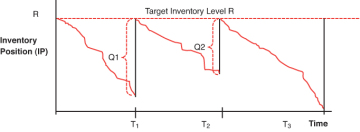
Figure 1-6 Fixed-time period system
- Q = R – IP
where:
- Q = order quantity
- R = target inventory level
- IP = inventory position
Two variables define this system and answer the two basic questions of when to order and how much: T and Q. They specify when to place an order: at time interval T. They also specify how much to order: quantity Q, computed as the difference between the target inventory, R, and the inventory position, IP. Sometimes this system is called the periodic review system to indicate that the inventory level is checked periodically, rather than continuously.
We can assume that an auto manufacturer uses a fixed-time period mode for its inventory of alternators. Also, let’s say its policy is to check inventory levels every two weeks, and that it has a target inventory level R = 5,000 alternators. If after two weeks the company checks its inventory level and finds its inventory position IP = 2,800 alternators, it would place an order for quantity Q = R – IP = 5,000 – 2,800 = 2,200 alternators. This is essentially how this policy system works.
The biggest difference between the fixed-order quantity system and the fixed-time period systems is in the timing and quantities of the orders placed. With the fixed-order quantity system inventory is checked on a continual basis and the system is prepared to place orders multiple times per year on a random basis. This has an advantage of providing greater system responsiveness, but it also requires administrative processes to be in place on a continual basis. In addition, as different inventory items reach their reorder points at different time periods, it might be difficult to obtain quantity discounts based on a bundled order.
The fixed-period order system requires carrying more safety stock inventory. The reason is that with this system we do not check the IP on a regular basis, and a sudden surge of demand could lead to a stockout. This system, however, allows more organized purchasing as inventory levels are checked in set time intervals. Orders can be bundled and quantity discounts obtained more easily, which can provide an advantage. In a fixed-order quantity system different items may reach reorder points at different times generating many orders at random intervals. On the other hand, a fixed-period system could ensure that inventory levels are checked on a regular basis for all items—say every two weeks. Then the orders for all the items could be bundled.