- 1.1 Introduction
- 1.2 Scope of Treatment
- 1.3 Analysis and Design
- 1.4 Conditions of Equilibrium
- 1.5 Definition and Components of Stress
- 1.6 Internal Force-Resultant and Stress Relations
- 1.7 Stresses on Inclined Sections
- 1.8 Variation of Stress Within a Body
- 1.9 Plane-Stress Transformation
- 1.10 Principal Stresses and Maximum in-plane Shear Stress
- 1.11 Mohr's Circle for Two-Dimensional Stress
- 1.12 Three-Dimensional Stress Transformation
- 1.13 Principal Stresses in Three Dimensions
- 1.14 Normal and Shear Stresses on an Oblique Plane
- 1.15 Mohr's Circles in Three Dimensions
- 1.16 Boundary Conditions in Terms of Surface Forces
- 1.17 Indicial Notation
- References
- Problems
Problems
Sections 1.1 through 1.8
1.1 |
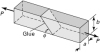
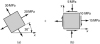
Two prismatic bars of a by b rectangular cross section are glued as shown in Fig. P1.1. The allowable normal and shearing stresses for the glued joint are 700 and 560 kPa, respectively. Assuming that the strength of the joint controls the design, what is the largest axial load P that may be applied? Use f = 40°, a = 50 mm, and b = 75 mm. |
||||||||||||
1.2 |
A prismatic steel bar of a = b = 50-mm square cross section is subjected to an axial tensile load P = 125 kN (Fig. P1.1). Calculate the normal and shearing stresses on all faces of an element oriented at (a) f = 70°, and (b) f = 45°. |
||||||||||||
1.3 |
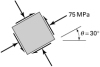
A prismatic bar is under an axial load, producing a compressive stress of 75 MPa on a plane at an angle q = 30° (Fig. P1.3). Determine the normal and shearing stresses on all faces of an element at an angle of q = 50°. |
||||||||||||
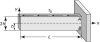
1.4 |
A square prismatic bar of 1300-mm2 cross-sectional area is composed of two pieces of wood glued together along the x' plane, which makes an angle q with the axial direction (Fig. 1.6a). The normal and shearing stresses acting simultaneously on the joint are limited to 20 and 10 MPa, respectively, and on the bar itself, to 56 and 28 MPa, respectively. Determine the maximum allowable axial load that the bar can carry and the corresponding value of the angle q. |
||||||||||||
1.5 |
Calculate the maximum normal and shearing stresses in a circular bar of diameter d = 50 mm subjected to an axial compression load of P = 150 kN through rigid end plates at its ends. |
||||||||||||
1.6 |
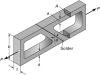
A frame is formed by two metallic rectangular cross sectional parts soldered along their inclined planes as illustrated in Fig. P1.6. What is the permissible axial load P all that can be applied to the frame, without exceeding a normal stress of s all or a shearing stress of t all on the inclined plane? Given: a = 10 mm, b = 75 mm, t = 20 mm, q = 55°, s all = 25 MPa, and t all = 12 MPa. Assumption: Material strength in tension is 90 MPa. |
||||||||||||
1.7 |
Redo Prob. 1.6 for the case in which s all = 20 MPa, t all = 8 MPa, and q = 40°. |
||||||||||||
1.8 |
Determine the normal and shearing stresses on an inclined plane at an angle f through the bar subjected to an axial tensile force of P (Fig. P1.1). Given: a = 15 mm, b = 30 mm, f = 50°, P = 120 kN. |
||||||||||||
1.9 |
Redo Prob. 1.8, for an angle of f = 30° and P = –100 kN. |
||||||||||||
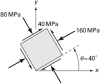
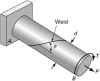
1.10 |
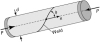
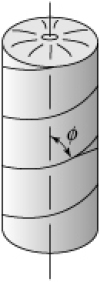
A cylindrical pipe of 160-mm outside diameter and 10-mm thickness, spirally welded at an angle of f = 40° with the axial (x) direction, is subjected to an axial compressive load of P = 150 kN through the rigid end plates (Fig. P1.10). Determine the normal s x' and shearing stresses t x'y' acting simultaneously in the plane of the weld. |
||||||||||||
1.11 |
The following describes the stress distribution in a body (in megapascals):
Determine the body force distribution required for equilibrium and the magnitude of its resultant at the point x = –10 mm, y = 30 mm, z = 60 mm. |
||||||||||||
1.12 |
Given zero body forces, determine whether the following stress distribution can exist for a body in equilibrium:
Here the c's are constants. |
||||||||||||
1.13 |
Determine whether the following stress fields are possible within an elastic structural member in equilibrium: The c's are constant, and it is assumed that the body forces are negligible. |
||||||||||||
1.14 |
For what body forces will the following stress field describe a state of equilibrium?
|
Sections 1.9 through 1.11
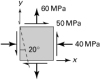
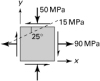
1.15 and 1.16 |
The states of stress at two points in a loaded body are represented in Figs. P1.15 and P1.16. Calculate for each point the normal and shearing stresses acting on the indicated inclined plane. As is done in the derivations given in Section 1.9, use an approach based on the equilibrium equations applied to the wedge-shaped element shown. |
1.17 and 1.18 |
Resolve Probs. 1.15 and 1.16 using Eqs. (1.18). |
1.19 |
At a point in a loaded machine, the normal and shear stresses have the magnitudes and directions acting on the inclined element shown in Fig. P1.19. What are the stresses s x , s y , and t xy on an element whose sides are parallel to the xy axes? |
1.20 |
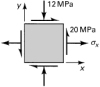
The stresses at a point in the enclosure plate of a tank are as depicted in the element of Fig. P1.20. Find the normal and shear stresses at the point on the indicated inclined plane. Show the results on a sketch of properly oriented element. |
1.21 |
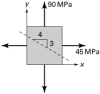
A welded plate carries the uniform biaxial tension illustrated in Fig. P1.21. Determine the maximum stress s for two cases: (a) The weld has an allowable shear stress of 30 MPa. (b) The weld has an allowable normal stress of 80 MPa. |
1.22 |
Using Mohr's circle, solve Prob. 1.15. |
1.23 |
Using Mohr's circle, solve Prob. 1.16. |
1.24 |
Using Mohr's circle, solve Prob. 1.20. |
1.25 |
Using Mohr's circle, solve Prob. 1.21. |
1.26 |
The states of stress at two points in a loaded beam are represented in Fig. P1.26a and b. Determine the following for each point: (a) The magnitude of the maximum and minimum principal stresses and the maximum shearing stress; use Mohr's circle. (b) The orientation of the principal and maximum shear planes; use Mohr's circle. (c) Sketch the results on properly oriented elements. Check the values found in (a) and (b) by applying the appropriate equations. |
1.27 |
By means of Mohr's circle, verify the results given by Eqs. (1.35). |
1.28 |
An element in plane stress (Fig. 1.3b) is subjected to stresses s x = 50 MPa, s y = –190 MPa, and t xy = –70 MPa. Determine the principal stresses and show them on a sketch of a properly oriented element. |
1.29 |
For an element in plane stress (Fig. 1.3b), the normal stresses are s x = 60 MPa and s y = –100 MPa. What is the maximum permissible value of shearing stress t xy if the shearing stress in the material is not to exceed 140 MPa? |
1.30 |
The state of stress on an element oriented at q = 60° is shown in Fig. P1.30. Calculate the normal and shearing stresses on an element oriented at q = 0°. |
1.31 |
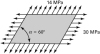
A thin skewed plate is subjected to a uniform distribution of stress along its sides, as shown in Fig. P1.31. Calculate (a) the stresses s x , s y , s xy , and (b) the principal stresses and their orientations. |
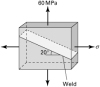
1.32 |
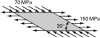
The stress acting uniformly over the sides of a rectangular block is shown in Fig. P1.32. Calculate the stress components on planes parallel and perpendicular to mn. Show the results on a properly oriented element. |
1.33 |
Redo Prob. 1.31 for the stress distribution shown in Fig. P1.33. |
1.34 |
A thin-walled cylindrical tank of radius r is subjected simultaneously to internal pressure p and a compressive force P through rigid end plates. Determine the magnitude of force P to produce pure shear in the cylindrical wall. |
1.35 |
A thin-walled cylindrical pressure vessel of radius 120 mm and a wall thickness of 5 mm is subjected to an internal pressure of p = 4 MPa. In addition, an axial compression load of P = 30p kN and a torque of T = 10p kN · m are applied to the vessel through the rigid end plates (Fig. P1.35). Determine the maximum shearing stresses and associated normal stresses in the cylindrical wall. Show the results on a properly oriented element. |
1.36 |
A pressurized thin-walled cylindrical tank of radius r = 60 mm and wall thickness t = 4 mm is acted on by end torques T = 600 N · m and tensile forces P (Fig. P1.35 with sense of P reversed). The internal pressure is p = 5 MPa. Calculate the maximum permissible value of P if the allowable tensile stress in the cylinder wall is 80 MPa. |
1.37 |
A shaft of diameter d carries an axial compressive load P and two torques T 1, T 2 (Fig. P1.37). Determine the maximum shear stress at a point A on the surface of the shaft. Given: d = 100 mm, P = 400 kN, T 1 = 10 kN · m, and T 2 = 2 kN · m. |
1.38 |
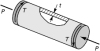
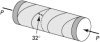
What are the normal and shearing stresses on the spiral weld of the aluminum shaft of diameter d subjected to an axial load P and a torque T (Fig. P1.38)? Given: P = 120 kN, T = 1.5 kN · m, d = 40 mm, and f = 50°. |
1.39 |
A hollow generator shaft of 180-mm outer diameter and 120-mm inner diameter carries simultaneously a torque T = 20 kN · m and axial compressive load P = 700 kN. What is the maximum tensile stress? |
1.40 |
A cantilever beam of thickness t is subjected to a constant traction t 0 (force per unit area) at its upper surface, as shown in Fig. P1.40. Determine, in terms of t 0, h, and L, the principal stresses and the maximum shearing stress at the corner points A and B. |
1.41 |
A hollow shaft of 60-mm outer diameter and 30-mm inner diameter is acted on by an axial tensile load of 50 kN, a torque of 500 N · m and a bending moment of 200 N · m Use Mohr's circle to determine the principal stresses and their directions. |
1.42 |
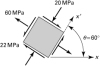
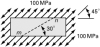
Given the stress acting uniformly over the sides of a thin, flat plate (Fig. P1.42), determine (a) the stresses on planes inclined at 20° to the horizontal and (b) the principal stresses and their orientations. |
1.43 |
A steel shaft of radius r = 75 mm is subjected to an axial compression P = 81 kN, a twisting couple T = 15.6 kN · m, and a bending moment M = 13 kN · m at both ends. Calculate the magnitude of the principal stresses, the maximum shear stress, and the planes on which they act in the shaft. |
1.44 |
A structural member is subjected to a set of forces and moments. Each separately produces the stress conditions at a point shown in Fig. P1.44. Determine the principal stresses and their orientations at the point under the effect of combined loading. |
1.45 |
Redo Prob. 1.44 for the case shown in Fig. P1.45. |
1.46 |
Redo Prob. 1.44 for the case shown in Fig. P1.46. |
1.47 |
The shearing stress at a point in a loaded structure is t xy = 40 MPa. Also, it is known that the principal stresses at this point are s 1 = 40 MPa and s 2 = –60 MPa. Determine s x (compression) and s y and indicate the principal and maximum shearing stresses on an appropriate sketch. |
1.48 |
The state of stress at a point in a structure is depicted in Fig. P1.48. Calculate the normal stress s and the angle q. |
1.49 |
Acting at a point on a horizontal plane in a loaded machine part are normal stress s y = 20 MPa and a (negative) shearing stress. One principal stress at the point is 10 MPa (tensile), and the maximum shearing stress is of magnitude 50 MPa. Find, by the use of Mohr's circle, (a) the unknown stresses on the horizontal and vertical planes and (b) the unknown principal stress. Show the principal stresses on a sketch of a properly oriented element. |
1.50 |
For a state of stress at a point in a structure, certain stress components are given for each of the two orientations (Fig. P1.50). Applying transformation equations, calculate stress components s y' and t x'y' and the angle q 1 between zero and 90°. |
1.51 |
A solid shaft 200 mm in diameter rotates at f = 20 rps and is subjected to a bending moment of 21p kN · m. Determine the torque T and power P that can also act simultaneously on the shaft without exceeding a resultant shearing stress of 56 MPa and a resultant normal stress of 98 MPa (with f expressed in rps and torque in N · m, P = 2p f · T in watts). |
1.52 |
The cylindrical portion of a compressed-air tank is made of 5-mm-thick plate welded along a helix at an angle of f = 60° with the axial direction (Fig. P1.52). The radius of the tank is 250 mm. If the allowable shearing stress parallel to the weld is 30 MPa, calculate the largest internal pressure p that may be applied. |
1.53 |
A thin-walled cylindrical tank is subjected to an internal pressure p and uniform axial tensile load P (Fig. P1.53). The radius and thickness of the tank are r = 0.45 m and t = 5 mm. The normal stresses at a point A on the surface of the tank are restricted to s x' = 84 MPa and s y' = 56 MPa, while shearing stress t x'y' is not specified. Determine the values of p and P. Use q = 30°. |
1.54 |
For a given state of stress at a point in a frame, certain stress components are known for each of the two orientations shown in Fig. P1.54. Using Mohr's circle, determine the following stress components: (a) t xy and (b) t x'y' and s y' . |
1.55 |
The state of stress at a point in a machine member is shown in Fig. P1.55. The allowable compression stress at the point is 14 MPa. Determine (a) the tensile stress s x and (b) the maximum principal and maximum shearing stresses in the member. Sketch the results on properly oriented elements. |
1.56 |
In Example 1.3, taking s z = 0, investigate the maximum shearing stresses on all possible (three-dimensional) planes. |
1.57 |
A thin-walled pressure vessel of 60-mm radius and 4-mm thickness is made from spirally welded pipe and fitted with two rigid end plates (Fig. P1.57). The vessel is subjected to an internal pressure of p = 2 MPa and a P = 50 kN a axial load. Calculate (a) the normal stress perpendicular to the weld; (b) the shearing stress parallel to the weld. |
1.58 |
A thin-walled cylindrical pressure vessel of 0.3-m radius and 6-mm wall thickness has a welded spiral seam at an angle of f = 30° with the axial direction (Fig. P1.10). The vessel is subjected to an internal gage pressure of p Pa and an axial compressive load of P = 9p kN applied through rigid end plates. Find the allowable value of p if the normal and shearing stresses acting simultaneously in the plane of welding are limited to 21 and 7 MPa, respectively. |
Sections 1.12 and 1.13
1.59 |
The state of stress at a point in an x, y, z coordinate system is Determine the stresses and stress invariants relative to the x', y', z' coordinate system defined by rotating x, y through an angle of 30° counterclockwise about the z axis. |
||||||||
1.60 |
Redo Prob. 1.59 for the case in which the state of stress at a point in an x, y, z coordinate system is |
||||||||
1.61 |
The state of stress at a point relative to an x, y, z coordinate system is given by Calculate the maximum shearing stress at the point. |
||||||||
1.62 |
At a point in a loaded member, the stresses relative to an x, y, z coordinate system are given by Calculate the magnitude and direction of maximum principal stress. |
||||||||
1.63 |
For the stresses given in Prob. 1.59, calculate the maximum shearing stress. |
||||||||
1.64 |
At a specified point in a member, the state of stress with respect to a Cartesian coordinate system is given by Calculate the magnitude and direction of the maximum principal stress. |
||||||||
1.65 |
At a point in a loaded structure, the stresses relative to an x, y, z coordinate system are given by Determine by expanding the characteristic stress determinant: (a) the principal stresses; (b) the direction cosines of the maximum principal stress. |
||||||||
1.66 |
The stresses (in megapascals) with respect to an x, y, z coordinate system are described by
At point (3, 1, 5), determine (a) the stress components with respect to x', y', z' if and (b) the stress components with respect to x", y", z" if |
||||||||
1.67 |
Determine the stresses with respect to the x', y', z' axes in the element of Prob. 1.64 if |
||||||||
1.68 |
For the case of plane stress, verify that Eq. (1.33) reduces to Eq. (1.20). |
||||||||
1.69 |
Obtain the principal stresses and the related direction cosines for the following cases: |
Sections 1.14 through 1.17
1.70 |
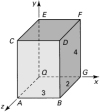
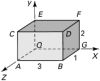
The stress at a point in a machine component relative to an x, y, z coordinate system is given by Referring to the parallelepiped shown in Fig. P1.70, calculate the normal stress s and the shear stress t at point Q for the surface parallel to the following planes: (a) CEBG, (b) ABEF, (c) AEG. [Hint: The position vectors of points G, E, A and any point on plane AEG are, respectively, r g = 3 i , r e = 4 j , r a = 2 k , r = x i + y j + z k . The equation of the plane is given by Equation P1.70
from which The direction cosines are then |
1.71 |
Re-solve Prob. 1.70 for the case in which the dimensions of the parallelepiped are as shown in Fig. P1.71. |
1.72 |
The state of stress at a point in a member relative to an x, y, z coordinate system is Determine the normal stress s and the shearing stress t on the surface intersecting the point and parallel to the plane: 2x + y – 3z = 9. |
1.73 |
For the stresses given in Prob. 1.62, calculate the normal stress s and the shearing stress t on a plane whose outward normal is oriented at angles 35°, 60°, and 73.6° with the x, y, and z axes, respectively. |
1.74 |
At a point in a loaded body, the stresses relative to an x, y, z coordinate system are Determine the normal stress s and the shearing stress t on a plane whose outward normal is oriented at angles of 40°, 75°, and 54° with the x, y, and z axes, respectively. |
1.75 |
Determine the magnitude and direction of the maximum shearing stress for the cases given in Prob. 1.69. |
1.76 |
The stresses at a point in a loaded machine bracket with respect to the x, y, z axes are given as Determine (a) the octahedral stresses; (b) the maximum shearing stresses. |
1.77 |
The state of stress at a point in a member relative to an x, y, z coordinate system is given by Calculate (a) the principal stresses by expansion of the characteristic stress determinant; (b) the octahedral stresses and the maximum shearing stress. |
1.78 |
Given the principal stresses s 1, s 2, and s 3 at a point in an elastic solid, prove that the maximum shearing stress at the point always exceeds the octahedral shearing stress. |
1.79 |
Determine the value of the octahedral stresses of Prob. 1.64. |
1.80 |
By using Eq. (1.38b), verify that the planes of maximum shearing stress in three dimensions bisect the planes of maximum and minimum principal stresses. Also find the normal stresses associated with the shearing plane by applying Eq. (1.37). |
1.81 |
A point in a structural member is under three-dimensional stress with s x = 100 MPa, s y = 20 MPa, t xy = 60 MPa, and s z , as shown in Fig. P1.81. Calculate (a) the absolute maximum shear stress for s z = 30 MPa; (b) the absolute maximum shear stress for s z = –30 MPa. |
1.82 |
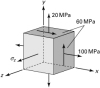
Consider a point in a loaded body subjected to the stress field represented in Fig. P1.82. Determine, using only Mohr's circle, the principal stresses and their orientation with respect to the original system. |
1.83 |
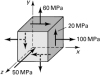
Re-solve Prob. 1.82 for the case of a point in a loaded body subjected to the following nonzero stress components: s x = 80 MPa, s z = –60 MPa, and t xy = 40 MPa. |
1.84 |
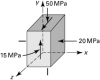
The state of stress at a point in a loaded structure is represented in Fig. P1.84. Determine (a) the principal stresses; (b) the octahedral stresses and maximum shearing stress. |
1.85 |
Find the normal and shearing stresses on an oblique plane defined by The principal stresses are s 1 = 35 MPa, s 2 = –14 MPa, and s 3 = –28 MPa. If this plane is on the boundary of a structural member, what should be the values of surface forces px , py , and px on the plane? |
1.86 |
Redo Prob. 1.85 for an octahedral plane, s 1 = 40 MPa, s 2 = 15 MPa, and s 3 = 25 MPa. |
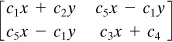
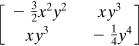




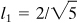 ,
, 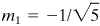 , and n
3 = 1. Show that the quantities given by Eq. (1.34) are invariant under the transformations (a) and (b).
, and n
3 = 1. Show that the quantities given by Eq. (1.34) are invariant under the transformations (a) and (b).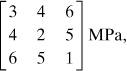

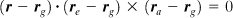
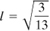 ,
, 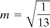 and
and 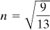 .
.