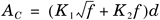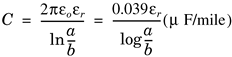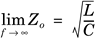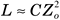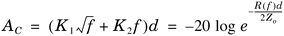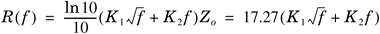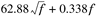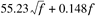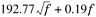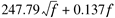This chapter is from the book
This chapter is from the book
This chapter is from the book
3.2 Coaxial Cable Model
Traditionally, the only attention that has been paid to signal attenuation has been the use of different types of coaxial cable. The primary parameters for twisted pair cables have been published, but similar information is not available for coaxial cables. To better understand the effects of termination and branch splitting when trying to identify a suitable transmission system for a high-throughput home network system over existing in-house TV signal wiring, we have attempted to estimate the primary parameters for coaxial cable. These estimates are based on cable loss measurements as well as cable physical dimensions. They are to be verified and improved by further experiments and measurements.
Signal attenuation of typical coaxial cables at a few different frequencies are summarized in Table 3.1. Attenuations are less than 10 dB at frequencies below 750 MHz for a coaxial cable of 100 feet. These cable losses, Ac, can be modeled by the following expression of two constant parameters.
)
In Equation 3.1, f is the frequency expressed in megahertz, K1 and K2 are parameters defining the coaxial cable type, and d is the cable length expressed in terms of kilofeet. K1 basically indicates the amount of conductor loss while K2 indicates the amount of dielectric loss. Modeling parameters for different type of cables are listed in Table 3.2. With this modeling expression and corresponding parameters, cable attenuations at different frequencies can be obtained.
To study termination and splitting branch effects, we can estimate the primary parameters of coaxial cables based on their physical dimensions and attenuation values. The shunt capacitance C of a coaxial cable can be calculated according to the geometry of the coaxial cable according to the following expression:
Table 3.1. Coaxial Cable Loss (dB)
|
Frequency (MHz) |
500-F |
625-F |
RG-6 |
RG-59 |
|---|---|---|---|---|
|
55 |
0.54 |
0.46 |
1.6 |
2.06 |
|
300 |
1.31 |
1.10 |
3.7 |
4.72 |
|
450 |
1.63 |
1.35 |
4.58 |
5.83 |
|
550 |
1.82 |
1.51 |
5.09 |
6.47 |
Table 3.2. Parameters of Cable Model
|
500-F |
625-F |
RG-6 |
RG-59 |
|
|---|---|---|---|---|
|
K1 |
0.69 |
0.6058 |
2.1144 |
2.7175 |
|
K2 |
0.0037 |
0.0016 |
0.0021 |
0.0015 |
)
where a is the diameter of the center conductor, b is the inside diameter of the outer conductor, and εr is the relative permeability. We assume εr = 1.
In addition, the characteristic impedance of a coaxial cable is almost constant and can be expressed in terms of serial inductance L and shunt capacitance C according to the following expression at high frequency:
)
Therefore, the serial inductance L can be estimated according to the following expression:
)
The coaxial cable attenuation can also be related to its serial resistance R according to the following expression:
)
Therefore, the serial resistance R can be estimated according to the following expression:
)
Table 3.3. Estimated Coaxial Cable Primary Parameters
|
500-F |
625-F |
RG-6 |
RG-59 |
|
|---|---|---|---|---|
|
a (inch) |
0.123 |
0.136 |
0.0403 |
0.032 |
|
b (inch) |
0.470 |
0.563 |
0.188 |
0.152 |
|
b/a |
3.82 |
4.14 |
4.67 |
4.75 |
|
R(ohms/mile) |
|
|
|
|
|
L(mH/mile) |
0.377 |
0.356 |
0.33 |
0.324 |
|
G |
0 |
0 |
0 |
0 |
|
C(μF/mile) |
0.067 |
0.0632 |
0.0587 |
0.0576 |
)
)
)
)
where we have assumed Z0 = 75ohms. Table 3.3 shows estimated coaxial cable primary parameters.
In Table 3.3, the frequency is expressed in megahertz. These estimates also assume that only the serial resistance R is a variable of frequency and the parallel conductance G is negligable. Figure 3.2 shows coaxial cable insertion losses for 500 feet of different types of cable, estimated according to these primary parameters.
)
Figure 3.2. Coaxial Cable Insertion Losses