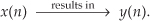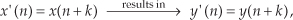- 1.1 Discrete Sequences and Their Notation
- 1.2 Signal Amplitude, Magnitude, Power
- 1.3 Signal Processing Operational Symbols
- 1.4 Introduction to Discrete Linear Time-Invariant Systems
- 1.5 Discrete Linear Systems
- 1.6 Time-Invariant Systems
- 1.7 The Commutative Property of Linear Time-Invariant Systems
- 1.8 Analyzing Linear Time-Invariant Systems
- References
- Chapter 1 Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.6 Time-Invariant Systems
A time-invariant system is one where a time delay (or shift) in the input sequence causes an equivalent time delay in the system's output sequence. Keeping in mind that n is just an indexing variable we use to keep track of our input and output samples, let's say a system provides an output y(n) given an input of x(n), or
Equation 1–23
For a system to be time invariant, with a shifted version of the original x(n) input applied, x'(n), the following applies:
Equation 1–24
where k is some integer representing k sample period time delays. For a system to be time invariant, Eq. (1–24) must hold true for any integer value of k and any input sequence.
1.6.1 Example of a Time-Invariant System
Let's look at a simple example of time invariance illustrated in Figure 1–9. Assume that our initial x(n) input is a unity-amplitude 1 Hz sinewave sequence with a y(n) output, as shown in Figure 1–9(b). Consider a different input sequence x'(n), where
Equation 1–25
)
Figure 1–9 Time-invariant system input/output relationships: (a) system block diagram, y(n) = –x(n)/2; (b) system input/output with a sinewave input; (c) input/output when a sinewave, delayed by four samples, is the input.
Equation (1–25) tells us that the input sequence x'(n) is equal to sequence x(n) shifted to the right by k = –4 samples. That is, x'(4) = x(0), x'(5) = x(1), x'(6) = x(2), and so on as shown in Figure 1–9(c). The discrete system is time invariant because the y'(n) output sequence is equal to the y(n) sequence shifted to the right by four samples, or y'(n) = y(n–4). We can see that y'(4) = y(0), y'(5) = y(1), y'(6) = y(2), and so on as shown in Figure 1–9(c). For time-invariant systems, the time shifts in x'(n) and y'(n) are equal. Take careful notice of the minus sign in Eq. (1–25). In later chapters, that is the notation we'll use to algebraically describe a time-delayed discrete sequence.
Some authors succumb to the urge to define a time-invariant system as one whose parameters do not change with time. That definition is incomplete and can get us in trouble if we're not careful. We'll just stick with the formal definition that a time-invariant system is one where a time shift in an input sequence results in an equal time shift in the output sequence. By the way, time-invariant systems in the literature are often called shift-invariant systems.†