- 2.1 The Time Domain
- 2.2 Sine Waves in the Frequency Domain
- 2.3 Shorter Time to a Solution in the Frequency Domain
- 2.4 Sine Wave Features
- 2.5 The Fourier Transform
- 2.6 The Spectrum of a Repetitive Signal
- 2.7 The Spectrum of an Ideal Square Wave
- 2.8 From the Frequency Domain to the Time Domain
- 2.9 Effect of Bandwidth on Rise Time
- 2.10 Bandwidth and Rise Time
- 2.11 What Does Significant Mean?
- 2.12 Bandwidth of Real Signals
- 2.13 Bandwidth and Clock Frequency
- 2.14 Bandwidth of a Measurement
- 2.15 Bandwidth of a Model
- 2.16 Bandwidth of an Interconnect
- 2.17 The Bottom Line
This chapter is from the book
This chapter is from the book
This chapter is from the book
2.15 Bandwidth of a Model
The simplest starting equivalent circuit model to represent a wire bond is an inductor. Up to what bandwidth might this be a good model? The only way to really tell is to compare a measurement with the prediction of this model. Of course, it will be different for different wire bonds.
As an example, we take the case of a very long wire bond, 300 mils long, connecting two pads over a return-path plane 10 mils below. This is diagrammed in Figure 2-17. A simple starting circuit model is a single ideal inductor and ideal resistor in series, such as shown in Figure 2-18. The best values for the L and R give a prediction for the impedance that closely matches the measured impedance up to 2 GHz. The bandwidth of this simple model is 2 GHz. This is shown in Figure 2-18.
)
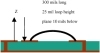
Figure 2-17 Diagram of a wire-bond loop between two pads, with a return path about 10 mils beneath the wire bond.
)
Figure 2-18 Top: Comparison of the measured impedance and the simulation based on the first-order model. The agreement is good up to a bandwidth of about 2 GHz. Bottom: Comparison of the measured impedance and the simulation based on the second-order model. The agreement is good up to a bandwidth of about 4 GHz. The bandwidth of the measurement is 10 GHz, measured with a GigaTest Labs Probe Station.
We could confidently use this simple model to predict performance of this physical structure in applications that had signal bandwidths of 2 GHz. It is surprising that for a wire bond this long, the simplest model, that of a constant ideal inductor and resistor, works so well up to 2 GHz. This is probably higher than the useful bandwidth of the wire bond, but the model is still accurate up to this high a frequency.
Suppose we wanted a model with an even higher bandwidth that would predict the actual impedance of this real wire bond to higher frequency. We might add the effect of the pad capacitance. Building a new model, a second-order model, and finding the best values for the ideal R, L, and C elements result in a simulated impedance that matches the actual impedance to almost 4 GHz. This is shown in Figure 2-18.