Produce Excel Charts That Look Like What You Had In Mind
Only a few minutes are required to learn the basics of Excel's charting module, but many frustrating hours are required to get a chart looking "just right." Most people create charts using one of the built-in chart types, but are unable to modify them to meet their exact requirements. This chapter introduces and explains the fundamental techniques we can use to impose our will on Excel's charting engine to produce charts that look exactly how we want them to.
The chapter focuses solely on the technical aspects of working with the chart engine. We do not investigate which chart type should be used in any given situation, nor the pros and cons of whether 3D charts can be used to present data accurately, nor whether you should use as few or as many of the colorful formatting options that Excel supports.
Fundamental Techniques
Combining Chart Types
When most people create charts, they start the Chart Wizard and browse through all the standard and custom chart types shown in Step 1, trying to find one that most closely resembles the look they're trying to achieve. More often than not, there isn't a close enough match and they end up thinking that Excel doesn't support the chart they're trying to create. In fact, we can include any number of column, bar, line, XY and/or area series within the same chart. All of the choices on the Custom Types tab of Step 1 of the Chart Wizard are no more than preformatted combinations of these basic styles, with a bit of formatting thrown in. Instead of relying on these custom types, we can usually get better results (and a greater understanding of the chart engine) by creating these combination charts ourselves. Unfortunately, we can't combine the different 3D styles, pie charts or bubble charts with other types.
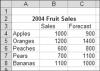
Let's start by creating a simple column/line combination chart for the data shown in Figure 15-1, where we want the 2004 sales to be shown as columns, with the forecast shown as lines.
 "
"
Figure 15-1 The Sample Data to Plot as a Combination Column/Line Chart
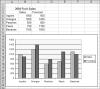
The easiest way to start is by selecting the data region, A3:C8 and create a simple column chart from it, as shown in Figure 15-2. We usually find it easiest to start with a column chart, but perhaps that's because it's the default selection in the Chart Wizard, so we can create the chart by selecting the source data, clicking the Chart Wizard toolbar button and then the Finish button on the Chart Wizard.
 "
"
Figure 15-2 The Chart Wizard Created a Standard Column Chart
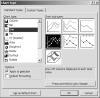
To change the Forecast values from a column to a line, select the series, click the Chart > Chart Type menu item and select one of the 2D Line chart types, choosing to apply the chart type to the selected series, as shown in Figure 15-3.
 "
"
Figure 15-3 Selecting the New Type for the Selected Series
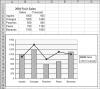
When you click OK, the Forecast series will display as a line, while the Sales series remains as the original column, as shown in Figure 15-4. (We've also modified the format of the Forecast line to make it stand out in the book.)
 "
"
Figure 15-4 The Resulting Combination Column/Line Chart
That's just about all there is to it. Start with a simple column chart with multiple series, select each series in turn, use the Chart > Chart Type menu to change its type and then apply the required formatting. The possible combinations are limited only by our imagination and the legibility of the final chart!
Using Multiple Axes
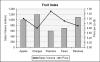
When we create one of the standard 2D charts, the plot area can have two sets of axes. The primary axes are usually displayed on the bottom and left, whereas the secondary axes are usually displayed on the top and right. If we have more than one series on the chart, we can choose which set of axes to use for each series by double-clicking the series and making our choice on the Axis tab of the Format Data Series dialog. When instructed to place a series on the secondary axis, Excel usually only displays a secondary Y axis on the chart. This can be changed using the Chart > Chart Options menu command, clicking the Axes tab and choosing whatever combination of primary and secondary axes are desired. When two series are plotted on different axes, the axes are scaled independently. Care must be taken to ensure that it is obvious to the viewer which series is plotted on which axis, by adding relevant axis labels and matching them to the series labels, as shown in Figure 15-5.
 "
"
Figure 15-5 Using Labels and Axis Titles to Clearly Identify Which Series Applies to Which Axis
Using Defined Names to Link Charts to Data
A key point to understand is that our charts do not have to refer directly to the cells containing their data. The source data for a chart series is provided by the =SERIES() function, which can be seen in the formula bar when a series is selected. The SERIES() function has the following format:
=SERIES(Name, XValues, YValues, PlotOrder)
Each of the four parameters can be a constant or array of constants, a direct range reference or a reference to a defined name. All the lines in Listing 15-1 are examples of valid functions.
Example 15-1. Examples of Valid SERIES() Functions
=SERIES(Sheet1!$B$1,Sheet1$A$2:$A$20,Sheet1!$B2:$B20,1)
=SERIES("Sales",Sheet1$A$2:$A$20,Sheet1!$B2:$B20,1)
=SERIES("Horizontal Line",{0,1},{123,123},1)
=SERIES("Book Names",Book1.xls!chtXName,Book1.xls!chtYName,1)
=SERIES("Sheet Names",Sheet1!chtXName,Sheet1!chtYName,1)
The last two versions of the SERIES() formula use workbook-level and sheet-level defined names respectively instead of direct cell references. This indirection enables us to use the defined names' definitions to modify the ranges or arrays passed to the chart, as shown in the following examples.
Setting Up the Defined Name Links
When you use a defined name in a SERIES formula, for best results you should begin with a name that references a worksheet range directly. After you have this working correctly, you can modify the name to perform more complex operations. Sometimes, if the formula for the defined name is particularly complex, or if we make an error in its definition, the charting module will refuse to accept the name in the SERIES() function. By starting with a very simple definition for the names, we are able to add them to the SERIES() function without problem.
Figure 15-6 shows a simple line chart, with the series selected and the SERIES() function displayed in the formula bar.
 "
"
Figure 15-6 A Simple Line Chart
To change the chart to use defined names, we first create two defined names, for the Date and Value ranges. Select Insert > Name > Define from the menu and create the following two names:
|
Name: |
Sheet1!chtDates |
|
Refers to: |
=Sheet1!$A$2:$A$9 |
|
Name: |
Sheet1!chtValues |
|
Refers to: |
=Sheet1!$B$2:$B$9 |
Now select the chart series and edit the SERIES() formula to read as follows:
=SERIES("Value",Sheet1!chtDates,Sheet1!chtValues,1)
That's it! The chart series is now linked to the defined names and the defined names refer to the source data ranges. Obviously, if we had more series in our chart, we would have to create extra names for the values for each additional series. Now that we've set up the linkage, we can modify the Refers To: formulas for the names (their definitions ) to create some interesting and time-saving effects.
Auto-Expanding Charts
One of the most frequently asked questions in the microsoft.public. excel.charting newsgroup is how to get a chart to automatically include new data as it's typed in. In Excel 2003, if we create a List from the data range and set either the chart or the defined names to refer to an entire column of the List, the reference will automatically be adjusted to include any new data. In previous versions, or if we prefer not to convert the range to a List in Excel 2003, we can use defined names to do the automatic updating.
The trick is to use a combination of the OFFSET() and COUNTA() functions in the definition of the name used for the X values, then define the name used for the Y values as an offset from the X values range. Select a cell in the worksheet, then choose Insert > Name > Define. Change the definition of the chtDates range to be the following by selecting the existing chtDates entry, typing the new definition and clicking the Add button:
|
Name: |
Sheet1!chtDates |
|
Refers to: |
=OFFSET(Sheet1!$A$2,0,0,COUNTA(Sheet1!$A:$A)-1,1) |
The OFFSET() function has the following parameters:
=OFFSET(SourceRange, RowsToMoveDown, ColumnsToMoveAcross,
NumberOfRowsToInclude, NumberOfColumnsToInclude)
The COUNTA() function returns the number of non-blank cells in the range, which in our case includes the header row. We therefore subtract one to get the number of data items. Putting the two together gives us a reference that starts in A2, moves down zero rows and across zero columns (so remains in A2), has a number of rows equal to the count of our data items and is one column wide. While in the Define Name dialog with the chtDates name selected, if we tab into the Refers to: box, Excel will highlight the resulting range with its "dancing ants," as shown in Figure 15-7.
 "
"
Figure 15-7 Excel's Dancing Ants Showing the Range Referred to by the Defined Name
While we're in the Define Name dialog, we need to modify the definition of the chtValues name. The easiest way to do that is to again use the OFFSET() function, but this time to start at the range referred to by the chtDates name and move one column across, keeping the same height and width:
|
Name: |
Sheet1!chtValues |
|
Refers to: |
=OFFSET(Sheet1!chtDates,0,1) |
After clicking OK to apply those changes and return to the worksheet, the chart should be showing exactly the same as before&8212;the new definitions resolve to the same ranges we started off with. The difference now is that if we type a new data point in row 10, it will automatically appear on the chart (assuming calculation is set to Automatic)!
To recap, it works because the COUNTA() function contained within the definition of the chtDates range returns the number of items in column A, which now includes the new entry. That feeds into the OFFSET() function, making it include the new entry in its resulting reference (now A2:A10). The chtValues range is updated to refer to one column across from the expanded chtDates range, so becomes B2:B10 and both those names feed into the chart series =SERIES() function, making the chart redraw to include the new data. The functions used in the defined name assume that the source data is contiguous, starting in cell A2. Blank cells will result in an incorrectly calculated range. More precise formulas are outside the scope of this book, but can easily be found by searching the Google newsgroup archives.
It is fundamental to the rest of this section that you fully understand the mechanism we're using. If anything is unclear, take some time to go through the example, perhaps trying to create an auto-expanding chart with two or three data series.
Scrolling and Zooming a Time Series
In the auto-expanding chart, we were only updating one of the OFFSET() function's parameters. If we modify both the row offset and number of rows, we can provide a simple, codeless mechanism for our users to scroll and zoom through a time series. In the worksheet shown in Figure 15-8, we've added two scrollbars from the Forms toolbar below the chart, set their Min and Max values to correspond to the number of data points and linked their values to the cells in column D, using two defined names ZoomVal and ScrollVal to refer to cells D24 and D25 respectively.
 "
"
Figure 15-8 Allowing the User to Zoom and Scroll Through Time-Series Data
In the definition for the chtDates name for this example, the ScrollVal figure is used for the row offset and the ZoomVal figure provides the number of data points to include in the range:
|
Name: |
Sheet1!chtDates |
|
Refers to: |
=OFFSET(Sheet1!$A$1,Sheet1!ScrollVal,0,Sheet1!ZoomVal,1) |
The chtValues definition is the same as before, =OFFSET(chtDates,0,1).
Transforming Coordinate Systems
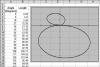
In the previous two examples, we've used the OFFSET() function in the defined name to change the range of values drawn on the chart, but keeping the actual data intact. We can also use defined names to modify the data itself prior to plotting it, such as transforming between polar and x, y coordinate systems. In polar coordinates, a point's location is defined by its angle and distance from the origin, rather than the distance-along and distance-up of the standard XY chart. Excel does not have a built-in chart type that will plot data in polar coordinates, but we can use defined names to convert the (angle, length) polar coordinate to (x, y), which can then be drawn on a standard XY chart. We're going to show you how to create the chart shown in Figure 15-9 from the data shown beside it by using defined names. In this example, the length figures are calculated from the angle using the formula a*sin(a).
 "
"
Figure 15-9 Plotting Polar Coordinates on an XY Scatter Chart
To demonstrate how the various uses of defined names can be combined, we'll implement two levels of indirection. The first level will use the technique from the Auto-Expanding Charts section above to automatically handle changing data sets, while a second level will perform the coordinate transformation.
The names to handle the automatic updates are defined as follows:
|
Name: |
Sheet1!datAngle |
|
Refers to: |
=OFFSET(Sheet1!$A$3,1,0,COUNTA(Sheet1!$A$3:$A$5000)-1,1) |
|
Name: |
Sheet1!datLength |
|
Refers to: |
=OFFSET(Sheet1!datAngle,0,1) |
The observant reader might have noticed that we're using a slight different version of the OFFSET() function in the definition for the datAngle name. The version shown here is slightly more robust, as it counts within a specific range of 5,000 cells, starting with the data header cell. You may have seen a variation on this technique in which the entire column address was used in the COUNTA function. By limiting the range in the way we do here, it doesn't matter whether the user changes the contents of the cells above the data range, such as adding extra titles to the sheet.
With the datAngle and datLength names referring to our source data, we can define two more names to convert from the polar to x, y coordinates:
|
Name: |
Sheet1!chtX |
|
Refers to: |
=Sheet1!datLength*COS(Sheet1!datAngle*PI()/180) |
|
Name: |
Sheet1!chtY |
|
Refers to: |
=Sheet1!datLength*SIN(Sheet1!datAngle*PI()/180) |
The chart series can then use the chtX and chtY names for the X and Y data:
=SERIES("Polar Plot",Sheet1!chtX,Sheet1!chtY,1)
Charting a Function
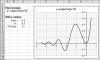
So we've used defined names to change the range of cells to plot and to manipulate the data in that range before we plot it. In Chapter 14 &8212; Data Manipulation Techniques, we introduced array formulas and explained how they can be used to perform calculations on arrays of data. We also showed a specific array formula that is often used to generate a number sequence for use in other array formulas. What we didn't mention was that we can also use array formulas in our defined names and refer to them from charts! Figure 15-10 shows a worksheet that uses array formulas in defined names to plot a mathematical function over a range of x values, without needing to read any data from the worksheet.
 "
"
Figure 15-10 Using Array Formulas in Defined Names to Generate and Plot Data
This worksheet combines a number of Excel tricks to generate the x axis values and use them to calculate the y axis results. We create a defined named to generate the values for the x axis and give it the name x, for reasons explained below:
|
Name: |
Sheet1!x |
|
Refers to: |
=$C$6+(ROW(OFFSET($A$1,0,0,$C$8,1))-1)*($C$7-$C$6)/($C$8-1) |
Working through the parts of this array formula:
- OFFSET($A$1,0,0, $C$8,1) gives the range A1:A51.
- ROW(OFFSET($A$1,0,0, $C$8,1)) converts the range to the array { 1, 2, 3, …, 50, 51}.
- (ROW(OFFSET($A$1,0,0, $C$8,1))-1) subtracts 1 from each item in the array, giving { 0, 1, 2, …, 49, 50}.
- ($C$7-$C$6)/($C$8-1) calculates the x axis increment for each point, giving 0.1 in our example.
- (ROW(OFFSET($A$1,0,0,$C$8,1))-1)*($C$7-$C$6)/($C$8-1) multiplies each item in the array by the x axis increment, giving the array { 0, 0.1, 0.2, …, 4.9, 5.0}.
- $C$6+(ROW(OFFSET($A$1,0,0,$C$8,1))-1)*($C$7-$C$6)/($C$8-1) adds the array to the required x value start point, resulting in the range of x values to use in the chart { –4.5, –4.4, –4.3, … 0.49, 0.50}.
Unfortunately, if we try to include Sheet1!x in the chart SERIES() function, we get an error about an incorrect range reference. To create the chart, we use the workaround described at the start of this section, by creating two names chtX and chtY that point to worksheet cells, use them to create the chart and then change them to their real definitions:
|
Name: |
Sheet1!chtX |
|
Refers to: |
=Sheet1!x |
|
Name: |
Sheet1!chtY |
|
Refers to: |
=EVALUATE(Sheet1!$B$3&"+x*0") |
The definition for chtX is just a workaround for Excel not allowing us to use the x name in the chart itself. The definition for chtY needs some explaining! Cell B3 contains the equation to be plotted, exp(x)*sin(x^2), as text. The EVALUATE function is an XLM macro function, equivalent to the VBA Application.Evaluate method, but which can be called from within a defined name. XLM functions were the programming language for Excel 4, replaced by VBA in Excel 5, but still supported in Excel 2003. The documentation for the XLM functions can be downloaded from the Microsoft Web site, by searching for "macrofun.exe" or "xlmacro.exe." At the time of writing, one version of the file is available from http://support.microsoft.com/?kbid=128175.
EVALUATE() evaluates the expression it's given, returning a numeric result. In our case, when the expression is evaluated, Excel replaces the x's in the formula with the array of values produced by our Sheet1!x defined name (which is exactly why we called it x) and returns an array containing the result of the function for each of our x axis values. These arrays are plotted on the chart, to give the line for the equation. The &"+x*0" part of the chtY definition works around an error in Excel that sometimes causes trig functions to not evaluate as array formulas, by forcing the entire formula to be evaluated as an array.
Faking It
A chart is a visual artifact, designed to impart information to the viewer in a graphical manner. As such, we should mainly be interested in whether the final chart looks correct and performs its purpose of providing clear information. We should not be too bothered about whether the chart has been constructed according to a notional set of generally approved guidelines. In other words, we often need to cheat by using some of the chart engine's features in "creative and imaginative" ways. This section explains a few ways in which we can get creative with Excel's chart engine, by using some of its features in ways they were probably not designed to be used.
Error Bars
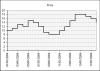
When is a line not a line? When it's an error bar! From a purely visual perspective, an error bar is a horizontal or vertical line emanating from a data point, so if we ever have the need to draw horizontal or vertical lines around our data points, we might consider using error bars for those lines. A great example is the step chart shown in Figure 15-11, where the vertical lines show the change in an item's price during a day and the horizontal lines connect the end price from one day to the start price for the next day.
 "
"
Figure 15-11 A Step Chart
Because Excel doesn't include a built-in Step Chart type, many people believe that Excel can't create them. There are quite a few ways in which it can be done, but the easiest is probably to use an XY chart with both vertical and horizontal error bars. The basic data for the chart consists of a list of dates and end-of-day prices, with a calculated field for the change in price from the end of the previous day. From this basic data, we start with a normal XY chart to plot the price against the date, as shown in Figure 15-12.
 "
"
Figure 15-12 Start with a Normal XY (Scatter) Chart of Price vs. Date
Below each data point, we want to display a vertical line equal to the change in price for that day, which we do by specifying a custom minus error value in the Y Error Bars tab of the Format Data Series Dialog, as shown in Figure 15-13.
 "
"
Figure 15-13 Add a Custom Minus Y Error Bar for the Day's Change in Price
The horizontal lines need to join each data point to the bottom of the subsequent point's error bar. That sounds difficult, but because these are daily prices all you need to do is add Plus markers to the X error bars with a fixed value setting of 1. With the error bars configured, you should be seeing a chart something like that shown in Figure 15-14.
 "
"
Figure 15-14 The Chart with the Additional Error Bars
All that remains is to double-click the error bar lines and use the Patterns tab to change their color, thickness and marker style, and then double-click the original XY line and format that to have no line and no marker. The result appears to be the step chart from Figure 15-11, even though it's actually only error bars being drawn.
Dummy XY Series
When is an axis not an axis? When it's an XY series with data labels! Excel's value axes are either boringly linear or logarithmic. They do not support breaks in the axis, nor scales that vary along the axis nor many other complex-axis effects. Figure 15-15 shows a chart with a variable Y axis, where the bottom half of the chart plots values from 0 to 100 in steps of 20, but the top half plots 100 to 1,000 in steps of 200:
 "
"
Figure 15-15 Chart with a Complex Axis Scale
In this chart, the real Y axis goes from zero to 200, but we've added a dummy XY series using the data from B10:C20, added data labels to the XY series, set them to display to the left of the point and customized their text to that shown in the figure. The result appears to be a complex axis scale that varies up the chart. The final step is to transform the real sales data in B3:B7 into the correct values for Excel to plot on its linear 0 to 200 scale, which is done using a simple mapping formula in C3:C7 of =IF(B3<=100,B3,100+B3/10), which is the data that Excel plots.
We can use this technique to implement any axis scale of our choosing, such as including breaks in our axes, plotting using logarithmic, hyperbolic or probability scales or even including multiple dummy XY series to make the chart appear to have many axes (as long as the user can determine which series is plotted against which axis). This effect can be misleading, if it is not clearly shown that a break in the axis scale exists. The chart in Figure 15-15 looks linear along its entire range, but if plotted on a true linear scale, it would resemble a boomerang with a large angle in the middle. An easy way to indicate a break in the axis is to set an individual point's data marker using a custom image, as we have done. Draw the image using Paint or other graphics program, copy it to the clipboard, select the data point and paste the image.