Troubleshoot Failure Domains and Information Hiding in your Networks
Information hiding relates to the larger goals, or policies, of building scalable, repeatable networks. This excerpt presents some widely used solution implementations.
Save 35% off the list price* of the related book or multi-format eBook (EPUB + MOBI + PDF) with discount code ARTICLE.
* See informit.com/terms
The intentional modification or shaping of traffic flows across a network is not the only kind of policy that network engineers must interact with. Information hiding, while not often considered a form of policy, relates to the larger goals, or policies, of building scalable, repeatable networks. These policies have consequences in terms of traffic flow, although these consequences are often unintentional rather than intentional—which means they are often ignored. This chapter and the next, Chapter 20, “Examples of Information Hiding,” are dedicated to considering this one problem, the solution space, and some widely used solution implementations. The first section in this chapter will examine the problem space, the second various kinds of solutions that can be used to counter the problem, and the third section will consider information hiding in the context of network complexity.
The Problem Space
Control planes are designed to learn about and carry as much information about the network topology and reachability as possible. Why would network engineers want to limit the scope of this state, once the processing and memory have been spent to learn it? There are several answers, including
To reduce resource utilization in devices participating in the control plane, generally just to save costs
To prevent a failure in one part of a network from impacting some other part of the network; in other words, to break up the network into failure domains
To prevent leaking information about the topology of the network, and reachability to destinations attached to the network, to attackers; in other words, to reduce the network’s attack surface
To prevent positive feedback loops that can cause a complete network failure
The problems in the preceding list can be divided into two categories: reducing the scope of control plane information and reducing the speed at which control plane information is allowed to change. These will be considered in the two following sections.
Defining Control Plane State Scope
Figure 19-1 illustrates the scope of control plane state.
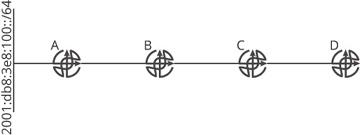
Figure 19-1 The scope of control plane state
There are two kinds of state carried by the control plane: topology and reachability. These two kinds of control plane state can have different scopes in a network. For instance:
If D has knowledge of 2001:db8:3e8:100::/64, then the scope of this reachability information is A, B, C, and D—the entire network.
If C has knowledge of 2001:db8:3e8:100::/64, and D does not, then the scope of this reachability information is A, B, and C.
If D knows about the link connecting A and B, or that A and B are adjacent, the scope of this topology information is A, B, C, and D—the entire network.
If D does not know about the link connecting A and B, or that A and B are adjacent, the scope of this topology information is A, B, and C.
Another way to look at this is to ask: if a link or reachability to a specific destination fails, which devices must participate in convergence? Any device that does not participate in convergence, perhaps by sending an update, recalculating the set of loop-free paths through the network, or switching to an alternate path, is not part of the failure domain. Any device that does need to send an update, recalculate the set of loop-free paths, or switch to an alternate path is part of the failure domain. The scope of a failure, then, determines the scope of the failure domain. In Figure 19-1:
If D has knowledge of 2001:db8:3e8:100::/64, then D must recalculate its set of reachable destinations if 100::/64 is disconnected from A; hence D is part of the failure domain for this destination.
If D does not have knowledge of 2001:db8:3e8:100:/64, then D does not change its local forwarding information when 100::/64 is disconnected from A; hence D is not part of the failure domain for this destination.
If D has knowledge of the link between A and B, then D needs to recalculate the set of loop-free paths through the network if the link fails (along with any reachability information passing through the link); hence D is part of the failure domain for this specific link.
If D does not have knowledge of the link between A and B, then D does not need to recalculate anything when the link fails; hence D is not part of the failure domain.
This definition means failure domains must be determined for each piece of reachability and topology information. While protocols and network designs will block reachability and/or topology at common points in a network, there are cases in which
Topology information is blocked, but not reachability information.
Some reachability information is blocked, but not all.
Some reachability or topology information leaks, causing a leaky abstraction.
The scope of control plane information within a network is important because it has a very large impact on the speed at which the control plane converges. Each additional device required to recalculate because of a change in topology or reachability represents some amount of time the network will remain unconverged, and hence either some destinations will be unnecessarily unreachable, or packets will be looped across some set of links in the network because some routers have a different view of the network topology than others. Looping, in particular, is a problem, because loops quite often have the potential to become positive feedback loops, which can cause the control plane to fail to converge permanently.
Positive Feedback Loops
Positive feedback loops are a bit harder to imagine than the scope of control plane information; Figure 19-2 illustrates.
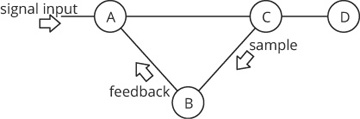
Figure 19-2 A sample circuit to illustrate positive feedback loops
In Figure 19-2, there are four devices:
Device A, which adds whatever it receives from the signal input and what it receives from B
Device B, which can either increase or decrease the size or frequency of the signal it receives from C
Device C, which passes the signal along unchanged to D, and also samples the signal, sending the sample to B
Device D, which measures the signal
To create a simple feedback loop, assume C samples some fraction of the signal passing through it, passing this sample to B. Device B, in turn, amplifies the sample by some factor, and passes this amplified signal back to A. Figure 19-3 shows the result.
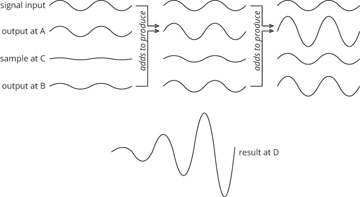
Figure 19-3 Result of a positive feedback loop
The case shown in Figure 19-3 is a positive feedback loop; C amplifies the sample it receives, making the signal just a bit larger. The result, at D, is a signal with constantly increasing amplitude. When will this feedback loop stop? When some limiting factor is hit. For instance, A may reach some limit where it cannot continue to add the two signals, or perhaps C reaches some input signal limit and fails, releasing its magic smoke (as all electronics will do if driven with too much input power). It is also possible to set up a negative feedback loop, where C removes a slight bit of power each cycle; in the case of a sine wave (as shown here), this would require C to invert the sample it receives from A. Finally, it is possible to configure each component in this circuit to neither increase nor decrease the final output at D. In this case, C would be somehow tuned to compensate for any inefficiency in the wiring, or A or C’s operation, by injecting just enough feedback to A to keep the signal at the same power at D.
Figure 19-4 changes the amplitude of the output signal to the frequency of an event to illustrate why.

Figure 19-4 Positive feedback loop using events
In Figure 19-4, B (as shown previously in Figure 19-2) is programmed to send a single event for every pair of events it receives. In the original signal input, there are six event signals, so B adds three more into the feedback path toward A. In the second round, shown in the center column, the original six events from the input signal are added to the three from B, resulting in nine event signals. Based on these nine event signals at the output of C, B will generate four event signals and feed them back to A. The result is that the output of A now has ten event signals. This increase in the number of signals will continue until the entire time space is saturated with event signals.
Physical and logical loops can cause links to become saturated, devices to run out of processing power or memory, or a number of other conditions that will eventually cause a network failure. Figure 19-5 is used to provide an example.
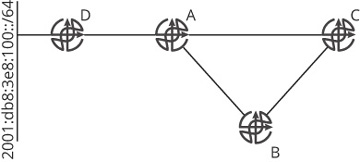
Figure 19-5 A permanent control plane failure due to a positive feedback loop
Assume that each router in Figure 19-5 is capable of processing ten changes to the network per second—either a route or topology change, for instance—and there are five routes total in the routing table. Because of the speeds of the interfaces (or for some other reason), the order in which updates are transmitted through the network is always [D,A,C,B]; updates from D through [A,C] always arrive at B before updates through [D,A] directly.
The 2001:db8:3e8:100::/64 link begins to flap three times per second. It seems like the network should converge on this flap rate fine; it is 50% of the rate at which any device can support, after all. To understand the impact of the feedback loop, however, it is important to trace the entire process of convergence:
Each time the 100:/64 link fails or comes up, D sends an update to A; this is three failures and three recoveries, for a total of six events per second.
For each of these events, D will send an update to A.
For each of these events, A will send an update to B and C.
B will also send an update toward C for each update it receives; this effectively doubles the rate of events at C to 12 per second.
During the first second C receives 12 events per second, it will fail, in turn taking down its relationships with A and B. When it comes back up, it will attempt to establish new adjacencies with each of the connected routers, which means it will send its entire database, containing five routes, to A and B. Given the 100::/64 link is still flapping at the same rate, this will drive B above its threshold, causing B to crash. It is possible, as well (depending on the timing), that A could crash.
Once A crashes, the chain of crashes through resource exhaustion will continue— if the timing is correct, or the crashes form their own self-supporting feedback loop, even if the original flapping link is repaired. Although feedback loops of this kind are not tagged as the root cause of the failure (the flapping link would be considered the root cause of the failure in this example), they are often what turns a single event into a complete failure of the control plane to converge.