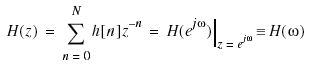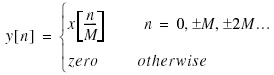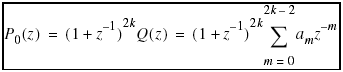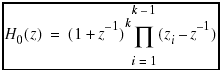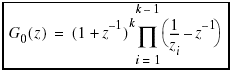Digital Filter Banks and the Wavelet Transform
- 1 Two-Channel Perfect Reconstruction Filter Banks
- 2 Orthogonal Filter Banks
- 3 General Tree-Structure Filter Banks and Wavelet Packets
In Chapter 5 we investigated the relationship between the wavelet transform and digital filter banks. It turns out that the wavelet transform can be simply achieved by a tree of digital filter banks, with no need of computing mother wavelets.1 Hence, the filter banks have been playing a central role in the area of wavelet analysis. In this chapter we will introduce the basics of filter banks.
The theory of filter banks was developed a long time ago, before modern wavelet analysis became popular. The reader can find many excellent textbooks in this area, such as Crochiere and Rabiner [12], Strang and Nguyen [47], and Vaidyanathan [48]. What will be introduced in this chapter are the fundamental concepts and designs of some of the most popular filter banks. They cover the majority of commonly used biorthogonal as well as orthogonal wavelets, except for the coiflets.
The Daubechies wavelets achieve the maximum number of wavelet zero moments, whereas the coiflets are a combination of wavelet zero moments and scaling function zero moments. The digital filters used to compute the coiflet wavelet transform cannot be generated by the structures discussed in this chapter. The design of digital filters for the coiflet wavelet transform needs some special skills and a certain level of mathematical preparation, which are beyond the scope of this book. The reader can find related information in the literature: [6], [13], [270], [247], [288], and [400].
Undoubtedly, experiments with new types of filter banks are proceeding, even as this book is being read. Nevertheless, this chapter provides an adequate tutorial for applied engineers and scientists who want to use wavelet analysis. It also can serve as an introduction for students who are new to the topic. While this chapter assumes some knowledge of the z-transform and digital filters, such knowledge is not essential. The basic principles of filter banks presented here are well developed and easily understood, so that even those with limited experience in wavelet analysis can quickly master this technique.
6.1 Two-Channel Perfect Reconstruction Filter Banks
In Section 5.3 we discussed the relationship between the scaling function, the mother wavelet, and filter banks. Once the lowpass and highpass filters have been determined, we can compute the scaling function and the mother wavelet through the refinement equations (5.40) and (5.65), respectively. Moreover, Section 5.4 further proves that under certain conditions the outputs of the highpass filters are good approximations of the wavelet series. Consequently, the selection of desired scaling functions and mother wavelets reduces to the design of lowpass and highpass filters of two-channel perfect reconstruction (PR) filter banks. The wavelet transform can simply be realized by a tree of two-channel PR filter banks. In this section we will briefly introduce the two-channel PR filter banks.
Figure 6-1 sketches a typical two-channel filter bank system,2 where the z-transform is defined as
(6.1)
Clearly, ω = 0 is equivalent to z = 1, and ω = p is equivalent to z = –1. Hence, H(0) and H(þ) in the frequency domain correspond to H(1) and H(–1) in the z-domain. In this book, we use N for the filter order. The length of the filter in Eq. (6.1) is equal to N + 1.
Figure 6-1 Two-channel filter bank. H0(z) and H1(z) form an analysis filter bank, whereas G0(z) and G1(z) form a synthesis filter bank. Note that H(z) and G(z) can be interchanged.
As shown in Figure 6-1, the signal X(z) is first filtered by a filter bank consisting of H0(z) and H1(z). The outputs of H0(z) and H1(z) are downsampled by 2 to obtain Y0(z) and Y1(z). After some processing, the modified signals are upsampled and filtered by another filter bank consisting of G0(z) and G1(z). The downsampling operators are decimetors and the upsampling operators are expanders. If no processing takes place between the two filter banks (in other words, Y0(z) and Y1(z) are not altered), the sum of the outputs of G0(z) and G1(z) is identical to the original signal X(z), except for a time delay. Such a system is commonly referred to as a two-channel perfect reconstruction filter bank. H0(z) and H1(z) form an analysis filter bank, whereas G0(z) and G1(z) form a synthesis filter bank. Note that H(z) and G(z) can be interchanged. For instance, we can use G0(z) and G1(z) for analysis and H0(z) and H1(z) for synthesis. In this book, H0(z) and G0(z) denote lowpass filters, while H1(z) and G1(z) are highpass filters. The subscripts 0 and 1 represent lowpass and highpass filters, respectively.
Note that for a discrete-time function x[n], the z-transform of its interpolated version is X(zM). This is because if
(6.2)
then
(6.3)
Similarly, the reader can verify that for a discrete-time function x[n], the z-transform of its doubly decimated version is
(6.4)
By applying the relations (6.3) and (6.4), we can derive the output of the lower channel in Figure 6-1 as
(6.5)
and the output of the upper channel as
(6.6)
Hence, the output will be
(6.7)
where one term involves X(z) and the other involves X(–z). For perfect reconstruction, the term with X(–z), traditionally called the alias term, must be zero. To achieve this, we need
(6.8)
which reminds us of Eq. (5.62). As a matter of fact, condition (5.62) can be considered as a special case of condition (6.8). While condition (6.8) leads to biorthogonal filter banks, (5.62) is the necessary condition for orthogonal filter banks.
To accomplish Eq. (6.8), we can let
(6.9)
which implies that γ0[n] can be obtained by alternating the sign of γ1[n]:
(6.10)
Similarly,
(6.11)
Therefore, γ1[n] and h1[n] are the highpass filters if γ0[n] and h0[n] are the lowpass filters. Once H0(z) and H1(z) [or G0(z) and G1(z)] are determined, we can find the remaining filters with Eq. (6.9).
For perfect reconstruction, we also need the first term in Eq. (6.7), called the distortion term, to be a constant or a pure time delay. For example,
(6.12)
where l denotes a time delay.3 If we satisfy both (6.8) and (6.12), the output of the two-channel filter bank in Figure 6-1 is a delayed version of the input signal
(6.13)
Let's rewrite (6.9) as
(6.14)
Substituting Eq. (6.14) into Eq. (6.12) yields
(6.15)
where P0(z) denotes the product of two lowpass filters, H0(z) and G0(z)
(6.16)
Eq. (6.15) indicates that all odd terms of the product of two lowpass filters, H0(z) and G0(z), must be zero, except for order l. But the even order terms are arbitrary. The delay parameter l must be odd, which is usually the center of the filter P0(z). We can summarize these observations by the following formula:
(6.17)
Consequently, the design of two-channel PR filter banks reduces to two steps:
Design a filter P0(z) that satisfies Eq. (6.17).
Factorize P0(z) into H0(z) and G0(z). Then, use Eq. (6.14) to compute H1(z) and G1(z).
Obviously, there are many ways to design P0(z). And there are many ways to factor it. The choice of four filters given by Eq. (6.9) is also not unique. Experiments are going on even as this book is being written, and undoubtedly they will still be on even as the book is being read. As an introduction to the wavelet transform, however, we will limit our presentation to those cases that are most popular in practical applications. The reader can find a more comprehensive treatment of filter banks in Strang and Nguyen [47] and Vaidyanathan [48].
One of the most well-known selections of the product filter P0(z) is defined by
(6.18)
The polynomial Q(z) of degree 2k – 2 is chosen so that Eq. (6.15) is satisfied. In this case, the order of P0(z) in (6.18) is always an even number. Moreover, it is a type I filter, i.e.,
(6.19)
which implies that the number of coefficients p0[n] is odd, N + 1. Based on Eq. (6.17), there are 2k – 1 odd powers in P0(z), and 2k – 1 coefficients to choose in Q(z). Thus, Q(z) is unique.
The special factor is also known as the binomial filter. The binomial itself, without Q(z), represents a spline filter. Q(z) is needed to give perfect reconstruction. It can be proved that 2k is the maximum number of zeros that P0(z) can have while preserving perfect reconstruction. Hence, P0(z) defined by Eq. (6.18) is traditionally named as the maxflat filter.
Example 6.1 A maxflat filter with k = 2 is
(6.20)
Since the order of Q(z) is 2k - 2 = 2, based on condition (6.17) we can compute
(6.21)
and
(6.22)
Hence, the two roots from Q(z) are at
(6.23)
While is inside unit the circle, its reciprocal is outside the unit circle. There are several possibilities for factoring P0(z) in (6.21). For example,
H0(z) = (1 + z-1)2 and G0(z) = (1 + z-1)2(c - z-1)(1/c - z-1). In this case, H0(z) has two zeros at z = –1 (that is, ω = þ), which is a typical quadratic spline, as shown in Figure 6-2.
Figure 6-2 Quadratic spline wavelets for case (a)
H0(z) = (1 + z-1)3 and G0(z) = (1 + z-1)(c - z-1)(1/c - z-1). In this case, H0(z) has three zeros at z = –1 (that is, ω = þ), which is a typical cubic spline. As shown in Figure 6-3, in this case, the analysis mother wavelet is much smoother than that corresponding to the quadratic spline in Figure 6-2. But the synthesis mother wavelet is less desirable. In both cases (a) and (b), all filters are linear phase. The resulting wavelets are both biorthogonal.
Figure 6-3 Cubic spline wavelets for case (b). Note that the cubic spline analysis mother wavelet is much smoother than that corresponding to the quadratic spline in Figure 6-2. But the corresponding synthesis mother wavelet is less desirable.
H0(z) = (1 + z-1)2(c - z-1) and G0(z) = (1 + z-1)2(1/c - z-1). This is the second order Daubechies mother wavelet, as shown in Figure 6-4. Unlike the spline wavelets, filters for the Daubechies mother wavelets are orthogonal. However, they do not have linear phase.
Figure 6-4 Daubechies 2 wavelets for case (c). The Daubechies filters are orthogonal and have the same length. The analysis and synthesis filters have similar behavior.
Example 6.1 demonstrates how to compute the product filter P0(z) and how to factor it. The common considerations of designing the lowpass FIR filters H0(z) and G0(z) include linear phase, minimum phase, and orthogonality. In many applications, such as image processing, linear phase is one of the most fundamental properties. In the time domain, linear phase implies that the coefficients of the causal filters are symmetric or antisymmetric around the central coefficient, i.e.,
(6.24)
In the z-transform domain, if zk is a zero, then so is 1/zk, zk*, and 1/z*k (assume that h[n] is real-valued). In other words, the zeros of a linear phase FIR filter H(z) occur in reciprocal conjugate pairs. Spline filters in cases (a) and (b) of Example 6.1 are all linear phase filters.
For FIR filters, minimum phase implies that all zeros lie inside the unit circle, i.e.,
(6.25)
The minimum phase filter possesses minimum phase-lag, but minimum phase has historically been the established terminology. Conversely, we name an FIR filter as a maximum phase filter if all its zeros lie outside the unit circle. For the Daubechies wavelets in Eqs. (6.26) and (6.27), while one has minimum phase, the other must have maximum phase. Obviously, no filter can have linear phase and minimum phase simultaneously.
Case (c), in fact, represents one of the most important classes in the wavelet family, the Daubechies wavelets. For the kth order Daubechies wavelets (which are commonly named Daubechies k wavelet or simply dbk),
(6.26)
and
(6.27)
It has been proved that for a given length of orthogonal filters (or given time support), the Daubechies wavelets filters achieve the maximum number of zeros at z = –1 (that is, ω = þ). Since the zeros of the lowpass filter H0(z) or G0(z) at z = –1 are related to the zero moments of the wavelet ψ(t) for a given time support, the Daubechies filters in Eqs. (6.26) and (6.27) possess the maximum number of vanishing moments.
For k = 1, the Daubechies wavelet is identical to the Haar wavelet. As the order k in (6.18) increases, the Daubechies wavelets become more and more smooth and also have more number of oscillations. On the other hand, as the order k increases, their time support becomes wider (see Figure 6-5).
Figure 6-5 As the order increases, the Daubechies wavelets appear more and more smooth and also have more oscillations. On the other hand, as the order increases, the time support becomes wider.
Figure 6-6 illustrates another set of popular scaling functions and wavelets that are employed for the FBI (Federal Bureau of Investigation) fingerprint compression. In this case,
(6.28)
Figure 6-6 Scaling functions and wavelets used for the FBI fingerprint compression
Figure 6-7 depicts the zero distribution of the corresponding lowpass filters, H0(z) and G0(z). Both of them have four zeros at þ. Since the pairs of reciprocals, zi and its reciprocal 1/zi (as well as zi* and its reciprocal 1/zi*), are assigned to the same filter, the resulting filters have linear phase.
Figure 6-7 Zero distribution of the pair of lowpass filters used for the FBI fingerprint compression. While the symbol "x" represents zeros of the analysis lowpass filter, the symbol "o" indicates zeros of the synthesis lowpass filter. The analysis and synthesis filters both have four zeros at p (that is, z = -1), respectively. Since the reciprocal pairs are assigned to the same filter, the resulting filters have linear phase.
As mentioned earlier, the derivations in this section are mainly based on the biorthogonal case (see Figure 6-1). The orthogonal transform, in fact, is a special case of its biorthogonal counterpart. In the next section we will investigate conditions, in terms of the product filter P0(z) and lowpass filters H0(z) or G0(z), for orthogonal wavelets.