Measuring Network Complexity
- Some Measures of Network Complexity
- Organized Complexity
- Is This a Waste of Time?
- A Final Thought
Given these four fundamental aspects of complexity—state, speed, surface, and optimization—it only makes sense to measure these four points and generate a single number describing the overall complexity of a given design and deployment structure. It would be nice if there were some way to examine a proposed network design, or a proposed change to a network design, and be able to assign actual numbers to the complexity of each component so the complexity can be compared to any potential gain in performance, or the loss of complexity in one area can be compared to the gain in complexity in another. If it were only that simple.
As it turns out, the effort to measure complexity is, itself, quite complex.
Two problems rise to the surface when examining the problem of measuring and quantifying a network toward gaining an understanding of the overall system complexity. First, there is the sheer amount of information available. Given the current push toward big data analytics, and the ability to measure thousands to millions of interactions and data mining to discover important trends and artifacts, shouldn’t something the size of an average network be an easy problem? Consider some of the various points of measurement just in trying to understand the interaction between the data flowing through each point in the network and the queuing mechanisms used to handle that traffic. This might include things such as:
- The amount of data flowing through each point in the network, including the input and output queue of each forwarding device.
- The depth and state of each queue of each forwarding device in the network.
- The source, destination, and other header information of each packet forwarded through the network.
- The number of packets dropped by each forwarding device, including the reason why they were dropped (tail drop, packet error, filtered, filtering rule, etc.).
Considering that the measurements themselves must pass through the network—and the measurements can easily contain more traffic than the measured traffic—the problems with measuring everything should quickly become apparent. How can you separate the measurement from the measured if the measurement is being carried on the same channel as what you are measuring? Added to this challenge are the states of each individual control plane system, and the components of those systems—things like the memory and processor utilization of each forwarding device, the state of each adjacency between each pair of devices participating in the control plane, and the flow of each reachability advertisement within the control plane. To make measuring the system complexity even more complex, the interactions between the systems must also somehow be taken into account—things like the impact of reachability information on the distribution and application of policy, any interdependencies between parallel control planes in terms of reachability information and system resources, and interactions between overlay and underlay control planes. Measuring not only the systems but also the interactions between the systems quickly becomes an intractable problem.
When measuring a system to understand its complexity level, some sort of sampling must take place. Sampling necessarily means that some information must be left out—which, in turn, means that any measurement of complexity along these lines is necessarily an abstract representation of the complexity, rather than a measure of the complexity itself.
To top all of this complexity off, there is very little agreement on the set of things to measure to create even an accurate abstract representation of the complexity of a network.
There is a second problem looming on the horizon just past this first one—a problem that’s not so obvious, and actually makes the problem of measuring network complexity intractable. Network design represents ordered (or intentional or organized—these three terms are often used interchangeably) complexity, rather than unordered complexity. While data analytics deals with unordered data well enough, ordered complexity is an entirely different problem set.
Let’s begin by examining some methods proposed to measure network complexity, and then consider ordered versus unordered complexity. Finally, several realms of complexity will be examined that will lead to practical applications.
Some Measures of Network Complexity
The difficulty of the task hasn’t stopped researchers from attempting to measure network complexity. Quite the opposite—there are a number of methods that have been tried over the years. Each of these methods has contributed useful thinking to the problem space, and can actually be used to provide some insight into what network complexity looks like. Overall, though, none of these measurements will truly provide a complete view of the complexity of a network.
Let’s look at three examples of network complexity measurements to get a feel for the space.
Network Complexity Index
The Network Complexity Index is described in “A Network Complexity Index for Networks of Networks”1 by Bailey and Grossman (commonly called the NCI). The general idea is to tackle describing network complexity in two steps:
Break the network down into subnetworks. As described in the original paper:
Given a network N, we first divide the network into smaller sub-networks C[1], . . ., C[j], . . . , C[p] with the property that two nodes selected at random from the sub-network C[i] are more likely to be connected to each other than two nodes selected at random from outside the sub-network (N\C).
Compute the complexity based on the size and number of the subnetworks. Again, as described in the original paper:
Given the sub-communities of the network N, let X[j] denote the size of the j largest sub-community, so that the sequence X[1], . . . , X[p] is in decreasing order. In general, different communities may have the same size. We define the network complexity index B(N) of the network N as the solution of the following equation: B(N) = Max j, X[j] j
The equation given is a standard statistic used in evaluating the importance of scientific research known as the H-index. The H-index determines the impact of a particular piece of research by evaluating the number of citations of the work in a way that is similar to a web page search index using the number of links to a page to determine the importance or relevance of that page.
Seen this way, the NCI attempts to combine the connectivity within a network with the number of nodes within a network:
- The more the subcommunities, the more connection points there must be between these subcommunities, and hence the more complex the connection graph must be.
- The larger the subcommunities, the more nodes there are within the network; this again impacts the implied connectivity graph of the network
The size and scope of the connectivity graph, in turn, impacts the way information flows within the network, which also relates to the complexity of the network.
What the NCI Does Well
The NCI does a good job of producing a single number that describes the size and shape of a network in terms of nodes and communities, in turn implying the scope and complexity of the network interconnections. This single number, computed over time, can help network managers and designers understand the growth of a network in terms other than sheer size.
What the NCI Doesn’t Do
From a network engineer’s perspective, there are several practical problems with using the NCI as a single measure of network complexity. First, this isn’t something you’re going to compute on a napkin while you’re eating dinner, or do rough calculations in your head around.2 This is a math heavy computation that requires automated tools to compute. Second, other than measuring the growth and interconnectedness of a topology, it’s hard to see how and where the NCI is useful in the real world. There’s no obvious way to reduce network complexity as measured by the NCI other than reducing the number and size of the subcommunities in the network.
This second objection, however, leads to another shortcoming of the NCI: it doesn’t really measure the complexity network operators interact with. It’s quite common, in the real world, to find very large networks supporting only a few workloads that have been heavily optimized for that workload, and hence are not very complex from an engineer’s point of view. It’s also quite common, in the real world, to find small networks with a very diverse workload, and hence cannot be optimized for a single workload. These networks are more complex than their size indicates—the NCI would likely underestimate the complexity of these networks.
So what does the NCI miss? Just those pieces of network architecture that designers deal with most of the time, such as:
- Policy, expressed through configuration, metrics, protocols, and other methods
- Resilience, expressed through the amount of redundancy, fast convergence mechanisms, and other highly complex design components
So while the NCI is useful, it doesn’t capture all the complexity of a single network in a way that can be usefully applied to real-world networks.
Modeling Design Complexity
In a set of slides presented to the Internet Research Task Force’s Network Complexity Research Group, a group of researchers described a model for measuring and describing the complexity of enterprise routing design.3 The process of measurement is as follows:
- Decompose the network design into individual pieces, implemented as individual configuration components (across all devices in the network).
- Build a network of connections between these individual components.
- Measure this network to determine the complexity of the configuration.
Figure 3.1 is taken from these slides,4 illustrating the linkages between the various configuration components.
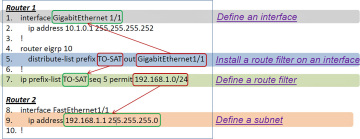
Figure 3.1 Evaluating Linkages in a Network Configuration
The more items configured, and the more dense the interconnection between the configurations (particularly between boxes), the more complex the design is determined to be. By examining these factors, the process yields a single number describing the complexity of the design. The presentation and the papers written by the same authors extend this concept to determining if the implemented design matches the design intent, given the design intent is stated in a way amenable to the process.
What Modeling Design Complexity Does Well
The concept of measuring not just the lines of configuration, but the interconnections between the lines of configuration, is extremely powerful. There is little doubt that much of complexity comes from the interrelated configurations spread throughout a network required to implement a single policy or to make a single protocol or process work. Looking at the interactions, or network of configurations, also takes the number of lines of configuration somewhat out of the picture as a measure of complexity. Because some devices can express a policy in a few simple lines, while others require a lot of configuration to express the same policy, this is a useful outcome.
What Modeling Design Complexity Doesn’t Do
At the same time, however, the interconnections between lines of configuration can fall prey to the same problems just counting the number of lines of configuration can fall prey to—an entire policy might be represented by a single line of configuration on one device, while requiring a number of lines of policy on another. For instance, on Cisco IOS Software, the command remove-private-as is used to remove any private AS numbers in a BGP route advertisement. This single command essentially replaces a set of configuration commands that would necessarily be interconnected, such as a filter and an application of that filter to a particular set of BGP peers. Both configurations are valid and perform the same set of actions, but they would appear to have completely different complexity levels according to the measure as it’s described. Further complicating the situation, different BGP implementations might use different sets of command to perform the same action, making one configuration appear more complex than another, although they’re both implementing the same policy.
Another failing of the measure described above is that it’s not always obvious what pieces fit together to make a policy. For instance, a configuration removing private AS numbers on every eBGP speaker in an AS might not appear to be related within the measurement; there is no specific point at which these multiple configurations overlap or interact in a way that’s obvious, unless you know the intent of the configuration. Thus some policies might easily be missed as they consist of configurations with no obvious point at which they tie together.
Finally, it’s difficult to assess how a single configuration used to implement multiple policies would be managed in this measure of network complexity—and yet, this is one of the thorniest problems to manage from a complexity standpoint, as this is precisely one of those difficult to manage interaction surfaces between otherwise unrelated policy implementations. How do the various policies measured interact? On this point, modeling design complexity is silent.
NetComplex
As previously discussed, the NCI measures complexity based on scale and perceived subcomponents; modeling design rates complexity on the network of interconnected lines of configuration. What about measuring complexity based on the amount of work needed to keep the distributed database that represents the network topology synchronized across all the devices participating in the control plane? This is precisely what NetComplex does. As Chun, Ratnasamy, and Kohler state:
- We conjecture that the complexity particular to networked systems arises from the need to ensure state is kept in sync with its distributed dependencies. The metric we develop in this paper reflects this viewpoint and we illustrate several systems for which this dependency centric approach appears to appropriately reflect system complexity.5
NetComplex evaluates the chain of dependent states in the network, assigns a metric to each dependency, and then calculates a single complexity measure based on these assigned metrics. Figure 3.2 illustrates dependency and complexity in NetComplex.
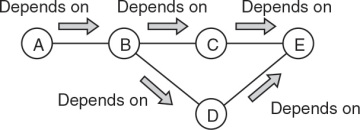
Figure 3.2 Dependency and Complexity in NetComplex
In this figure:
- Routers C and D depend on E to obtain a correct view of the network beyond Router E.
- Router B depends on Routers C, D, and E to obtain a correct view of the network beyond Router E.
- Router A depends on Routers B, C, D, and E to obtain a correct view of the network beyond Router E.
Hence, Router A “accumulates” the complexity of synchronization of information originating beyond E through the entire network. Through these dependencies, Router A is said to be linked to the remaining routers in the network. By examining these links, and combining them with the local state, the complexity of keeping the entire control plane synchronized can be given a single metric.
What NetComplex Does Well
By focusing on the amount of state and the way state is carried through the network, NetComplex does a good job of describing the complexity of a control plane. Based on this, NetComplex is useful for determining the additional complexity required to carry source routing information through the network, and forward based on this source routing information. Another place where Netcomplex would be useful is in putting a metric on the additional state information required to forward traffic on a per flow, rather than per destination/virtual topology basis.
What NetComplex Doesn’t Do
NetComplex, however, is focused on the control plane within a single administrative or failure domain. There is no way, for instance, to account for the information hidden through route aggregation, nor to differentiate between topology information and reachability (such as what happens at a link state flooding domain boundary). NetComplex doesn’t work with policies, nor policy implementation; nor does it deal with traffic flows, subnetwork scale, or network density.