Gas Laws: Pressure, Volume, and Temperature
- 4.1 Boyle’s Law
- 4.2 Charles’s Law
- 4.3 Absolute Temperature
- 4.4 The Ideal Gas Law
- 4.5 Real Gases
- 4.6 Volumetric Fractions and Mole Fractions
- 4.7 Standard Conditions
- 4.8 Concluding Comments
- Appendix 4A: Equations of State
- Problems
The majority of process operations involve material that is in a gaseous state. Temperatures can range from –150°F to over 1,400°F with pressures ranging from a vacuum to over 2,000 psi. These conditions are not isolated extremes, but rather conditions that are typically encountered in various hydrocarbon processing units. Given this wide range of operating conditions, it is critical that a process technologist understand the behavior of gases under extreme conditions.
Under “normal” conditions, all gases behave very much like an ideal gas. Those normal conditions range from about a few tens of degrees below 0°F to only several hundred degrees above, and with pressures from a vacuum to only a few atmospheres. However, as just noted, many processes are carried out under conditions that are anything but normal. As we will see, much can be learned about the nature of gases by studying “ideal” gases.
In general, the molecules, or atoms in the cases of the inert gases, are widely spaced. Consequently, their relatively small volume is insignificant and does not interfere with the relationships of pressure, volume, and temperature that we refer to as PVT. But under the extreme conditions of high pressure and low temperature just described, that molecular volume does interfere and causes a gas to behave in a nonideal manner that results in a larger volume. In addition, certain gases, such as Freon coolants, have strong intermolecular forces between the molecules that make them behave in a nonideal manner under less extreme conditions. Those intermolecular forces can be attractive, repulsive, or both, causing the volume to be smaller or larger.
4.1 Boyle’s Law
Simply stated, at a constant temperature the volume and absolute pressure of a gas’s given mass are inversely proportional. That is, if the volume of that gas’s given mass gas were to be changed by a certain factor, the absolute pressure would be increased by the inverse of that factor. This is known as Boyle’s Law and is applicable whether the volume is being increased or decreased. It only holds true for ideal gases.
Putting Boyle’s Law into a mathematical expression gives Equation 4.1.
Equation 4.1
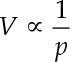
In this equation, p is the absolute pressure and V is the volume of a constant amount of gas in terms of either moles or mass. The ∝ symbol means that the left side of the equation is proportional to the right side. Think of this symbol as a “proportionality” symbol instead of an “equals” symbol. Figure 4.1 plots the volume of a constant mass amount of gas versus its absolute pressure at a constant temperature and shows the inverse proportional relationship of Equation 4.1.
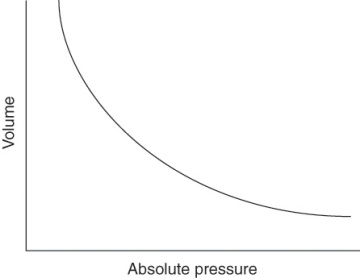
Figure 4.1 Plot of volume V versus pressure p of a gas at a constant temperature
Equation 4.1 implies that at constant temperature, the product of the absolute pressure times the volume is a constant for an ideal gas. This equation can be rewritten to show the effect of a before and after change of pressure and volume at constant temperature, giving us Equation 4.2.
Equation 4.2
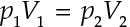
The subscripts 1 and 2 indicate the states before and after a change. Note that the change may be a change of absolute pressure, a change of volume, or a combination of both.
Stated another way, the product of the absolute pressure times the volume for a given amount of an ideal gas always remains constant for ideal gases.
Equation 4.2 can also be rewritten as shown in Equation 4.3.
Equation 4.3
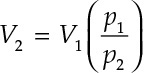
Similarly, it can be arranged as Equation 4.4.
Equation 4.4
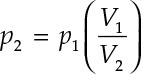
The subscript of 2 denotes the after condition and the subscript of 1 denotes the before condition.
Also note that a lower case letter p is used for the absolute pressure. We are following the practice of chemical engineers who also use the uppercase fancy script version letter P to denote that the pressure represents the combined effect of static pressure and gravitational forces taking into account the density of the fluid and its relative height. The pressure that is due to a column of fluid above a pressure point is given by Equation 4.5.
Equation 4.5
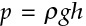
In this equation, p is the pressure caused by the fluid above the pressure point, ρ is the density of that fluid above the pressure point, g is the gravitational acceleration constant, and h is the total height of the fluid above the pressure point. Note that fluid below the pressure point has no contribution to the pressure; only the height of the fluid above the pressure point affects the pressure.