Defining Functions in Python
YOU HAVE BEEN COMPOSING CODE THAT calls Python functions since the beginning of this book, from writing strings with stdio.writeln() to using type conversion functions such as str() and int() to computing mathematical functions such as math.sqrt() to using all of the functions in stdio, stddraw, and stdaudio. In this section, you will learn how to define and call your own functions.
In mathematics, a function maps an input value of one type (the domain) to an output value of another type (the range). For example, the square function f(x) = x2 maps 2 to 4, 3 to 9, 4 to 16, and so forth. At first, we work with Python functions that implement mathematical functions, because they are so familiar. Many standard mathematical functions are implemented in Python’s math module, but scientists and engineers work with a broad variety of mathematical functions, which cannot all be included in the module. At the beginning of this section, you will learn how to implement and use such functions on your own.
Later, you will learn that we can do more with Python functions than implement mathematical functions: Python functions can have strings and other types as their domain or range, and they can have side effects such as writing output. We also consider in this section how to use Python functions to organize programs and thereby simplify complicated programming tasks.
From this point forward, we use the generic term function to mean either Python function or mathematical function depending on the context. We use the more specific terminology only when the context requires that we do so.
Functions support a key concept that will pervade your approach to programming from this point forward: Whenever you can clearly separate tasks within a computation, you should do so. We will be overemphasizing this point throughout this section and reinforcing it throughout the rest of the chapter (and the rest of the book). When you write an essay, you break it up into paragraphs; when you compose a program, you break it up into functions. Separating a larger task into smaller ones is much more important when programming than when writing an essay, because it greatly facilitates debugging, maintenance, and reuse, which are all critical in developing good software.
Using and defining functions
As you know from the functions you have been using, the effect of calling a Python function is easy to understand. For example, when you place math.sqrt(a-b) in a program, the effect is as if you had replaced that code with the return value that is produced by Python’s math.sqrt() function when passed the expression a-b as an argument. This usage is so intuitive that we have hardly needed to comment on it. If you think about what the system has to do to create this effect, however, you will see that it involves changing a program’s control flow. The implications of being able to change the control flow in this way are as profound as doing so for conditionals and loops.
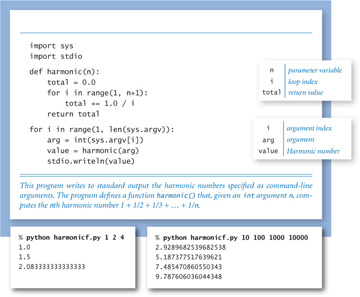
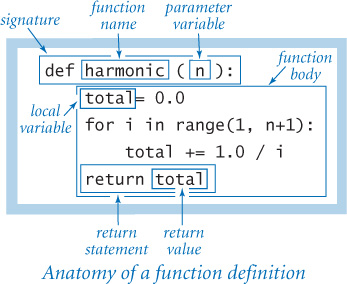
You can define functions in any Python program, using the def statement that specifies the function signature, followed by a sequence of statements that constitute the function. We will consider the details shortly, but begin with a simple example that illustrates how functions affect control flow. Our first example, PROGRAM 2.1.1 (harmonicf.py), includes a function named harmonic() that takes an argument n and computes the nth harmonic number (see PROGRAM 1.3.5). It also illustrates the typical structure of a Python program, having three components:
- A sequence of import statements
- A sequence of function definitions
- Arbitrary global code, or the body of the program
PROGRAM 2.1.1 has two import statements, one function definition, and four lines of arbitrary global code. Python executes the global code when we invoke the program by typing python harmonicf.py on the command line; that global code calls the harmonic() function defined earlier.
The implementation in harmonicf.py is preferable to our original implementation for computing harmonic numbers (PROGRAM 1.3.5) because it clearly separates the two primary tasks performed by the program: calculating harmonic numbers and interacting with the user. (For purposes of illustration, we have made the user-interaction part of the program a bit more complicated than in PROGRAM 1.3.5.) Whenever you can clearly separate tasks within a computation, you should do so. Next, we carefully examine precisely how harmonicf.py achieves this goal.
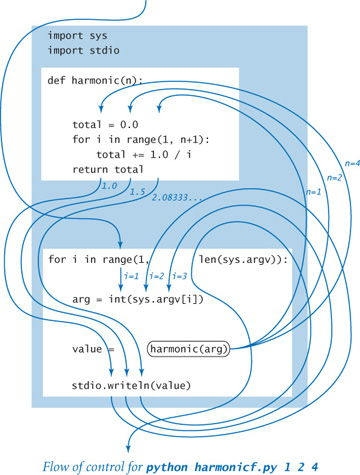
Control flow
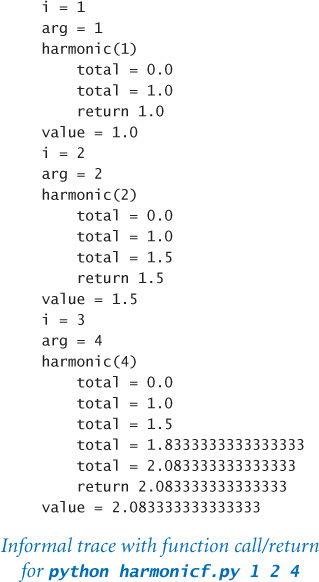
The diagram on the next page illustrates the flow of control for the command python harmonicf.py 1 2 3. First, Python processes the import statements, thus making all of the features defined in the sys and stdio modules available to the program. Next, Python processes the definition of the harmonic() function at lines 4 through 8, but does not execute the function—Python executes a function only when it is called. Then, Python executes the first statement in the global code after the function definition, the for statement, which proceeds normally until Python begins to execute the statement value = harmonic(arg), starting by evaluating the expression harmonic(arg) when arg is 1. To do so it transfers control to the harmonic() function—the flow of control passes to the code in the function definition. Python initializes the “parameter” variable n to 1 and the “local” variable total to 0.0 and then executes the for loop within harmonic(), which terminates after one iteration with total equal to 1.0. Then, Python executes the return statement at the end of the definition of harmonic(), causing the flow of control to jump back to the calling statement value = harmonic(arg), continuing from where it left off, but now with the expression harmonic(arg) replaced by 1.0. Thus, Python assigns 1.0 to value and writes it to standard output. Then, Python iterates the loop once more, and calls the harmonic() function a second time with n initialized to 2, which results in 1.5 being written. The process is then repeated a third time with arg (and then n) equal to 4, which results in 2.083333333333333 being written. Finally, the for loop terminates and the whole process is complete. As the diagram indicates, the simple code masks a rather intricate flow of control.
Program 2.1.1 Harmonic numbers (revisited) (harmonicf.py)
Informal function call/return trace
One simple approach to following the control flow through function calls is to imagine that each function writes its name and argument(s) when it is called and its return value just before returning, with indentation added on calls and subtracted on returns. The result enhances the process of tracing a program by writing the values of its variables, which we have been using since SECTION 1.2. An informal trace for our example is shown at right. The added indentation exposes the flow of the control, and helps us check that each function has the effect that we expect. Generally, adding calls on stdio.writef() to trace any program’s control flow in this way is a fine approach to begin to understand what it is doing. If the return values match our expectations, we need not trace the function code in detail, saving us a substantial amount of work.
FOR THE REST OF THIS CHAPTER, your programming will be centered on creating and using functions, so it is worthwhile to consider in more detail their basic properties and, in particular, the terminology surrounding functions. Following that, we will study several examples of function implementations and applications.
Basic terminology
As we have been doing throughout, it is useful to draw a distinction between abstract concepts and Python mechanisms to implement them (the Python if statement implements the conditional, the while statement implements the loop, and so forth). There are several concepts rolled up in the idea of a mathematical function and there are Python constructs corresponding to each, as summarized in the table at the top of the following page. While you can rest assured that these formalisms have served mathematicians well for centuries (and have served programmers well for decades), we will refrain from considering in detail all of the implications of this correspondence and focus on those that will help you learn to program.
When we use a symbolic name in a formula that defines a mathematical function (such as f(x) = 1 + x + x2), the symbol x is a placeholder for some input value that will be substituted into the formula to determine the output value. In Python, we use a parameter variable as a symbolic placeholder and we refer to a particular input value where the function is to be evaluated as an argument.
concept |
Python construct |
description |
function |
function |
mapping |
input value |
argument |
input to function |
output value |
return value |
output of function |
formula |
function body |
function definition |
independent variable |
parameter variable |
symbolic placeholder for input value |
Function definition
The first line of a function definition, known as its signature, gives a name to the function and to each parameter variable. The signature consists of the keyword def; the function name; a sequence of zero or more parameter variable names separated by commas and enclosed in parentheses; and a colon. The indented statements following the signature define the function body. The function body can consist of the kinds of statements that we discussed in CHAPTER 1. It also can contain a return statement, which transfers control back to the point where the function was called and returns the result of the computation or return value. The body may also define local variables, which are variables that are available only inside the function in which they are defined.
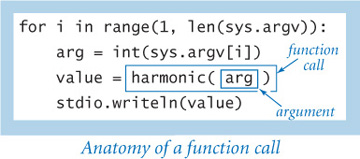
Function calls
As we have seen throughout, a Python function call is nothing more than the function name followed by its arguments, separated by commas and enclosed in parentheses, in precisely the same form as is customary for mathematical functions. As noted in SECTION 1.2, each argument can be an expression, which is evaluated and the resulting value passed as input to the function. When the function finishes, the return value takes the place of the function call as if it were the value of a variable (perhaps within an expression).
Multiple arguments
Like a mathematical function, a Python function can have more than one parameter variable, so it can be called with more than one argument. The function signature lists the name of each parameter variable, separated by commas. For example, the following function computes the length of the hypotenuse of a right triangle with sides of length a and b:
def hypot(a, b)
return math.sqrt(a*a + b*b)
Multiple functions
You can define as many functions as you want in a .py file. The functions are independent, except that they may refer to each other through calls. They can appear in any order in the file:
def square(x):
return x*x
def hypot(a, b):
return math.sqrt(square(a) + square(b))
However, the definition of a function must appear before any global code that calls it. That is the reason that a typical Python program contains (1) import statements, (2) function definitions, and (3) arbitrary global code, in that order.
Multiple return statements
You can put return statements in a function wherever you need them: control goes back to the calling program as soon as the first return statement is reached. This primality-testing function is an example of a function that is natural to define using multiple return statements:
def isPrime(n):
if n < 2: return False
i = 2
while i*i <= n:
if n % i == 0: return False
i += 1
return True
Single return value
A Python function provides only one return value to the caller (or, more precisely, it returns a reference to one object). This policy is not as restrictive as it might seem, because Python data types can contain more information than a single number, boolean, or string. For example, you will see later in this section that you can use arrays as return values.
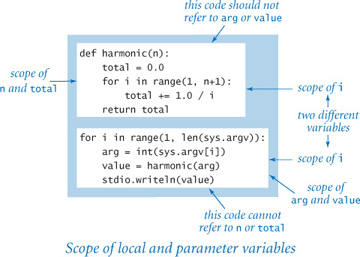
Scope
The scope of a variable is the set of statements that can refer to that variable directly. The scope of a function’s local and parameter variables is limited to that function; the scope of a variable defined in global code—known as a global variable—is limited to the .py file containing that variable. Therefore, global code cannot refer to either a function’s local or parameter variables. Nor can one function refer to either the local or parameter variables that are defined in another function. When a function defines a local (or parameter) variable with the same name as a global variable (such as i in PROGRAM 2.1.1), the variable name in the function refers to the local (or parameter) variable, not the global variable.
A guiding principle when designing software is to define each variable so that its scope is as small as possible. One of the important reasons that we use functions is so that changes made to one part of a program will not affect an unrelated part of the program. So, while code in a function can refer to global variables, it should not do so: all communication from a caller to a function should take place via the function’s parameter variables, and all communication from a function to its caller should take place via the function’s return value. In SECTION 2.2, we consider a technique for removing most global code, thereby limiting scope and the potential for unexpected interactions.
Default arguments
A Python function may designate an argument to be optional by specifying a default value for that argument. If you omit an optional argument in a function call, then Python substitutes the default value for that argument. We have already encountered a few examples of this feature. For example, math.log(x, b) returns the base-b logarithm of x. If you omit the second argument, then b defaults to math.e—that is, math.log(x) returns the natural logarithm of x. It might appear that the math module has two different logarithm functions, but it actually has just one, with an optional argument and a default value.
You can specify an optional argument with a default value in a user-defined function by putting an equals sign followed by the default value after the parameter variable in the function signature. You can specify more than one optional argument in a function signature, but all of the optional arguments must follow all of the mandatory arguments.
For example, consider the problem of computing the nth generalized harmonic number of order r: Hn, r = 1 + 1/2r + 1/3r + ... + 1/nr. For example, H1, 2 = 1, H2, 2 = 5/4, and H2, 2 = 49/36. The generalized harmonic numbers are closely related to the Riemann zeta function from number theory. Note that the nth generalized harmonic number of order r = 1 is equal to the nth harmonic number. Therefore it is appropriate to use 1 as the default value for r if the caller omits the second argument. We specify by writing r=1 in the signature:
def harmonic(n, r=1):
total = 0.0
for i in range(1, n+1):
total += 1.0 / (i ** r)
return total
With this definition, harmonic(2, 2) returns 1.25, while both harmonic(2, 1) and harmonic(2) return 1.5. To the client, it appears that we have two different functions, one with a single argument and one with two arguments, but we achieve this effect with a single implementation.
Side effects
In mathematics, a function maps one or more input values to some output value. In computer programming, many functions fit that same model: they accept one or more arguments, and their only purpose is to return a value. A pure function is a function that, given the same arguments, always return the same value, without producing any observable side effects, such as consuming input, producing output, or otherwise changing the state of the system. So far, in this section we have considered only pure functions.
However, in computer programming it is also useful to define functions that do produce side effects. In fact, we often define functions whose only purpose is to produce side effects. An explicit return statement is optional in such a function: control returns to the caller after Python executes the function’s last statement. Functions with no specified return value actually return the special value None, which is usually ignored.
For example, the stdio.write() function has the side effect of writing the given argument to standard output (and has no specified return value). Similarly, the following function has the side effect of drawing a triangle to standard drawing (and has no specified return value):
def drawTriangle(x0, y0, x1, y1, x2, y2):
stddraw.line(x0, y0, x1, y1)
stddraw.line(x1, y1, x2, y2)
stddraw.line(x2, y2, x0, y0)
It is generally poor style to compose a function that both produces side effects and returns a value. One notable exception arises in functions that read input. For example, the stdio.readInt() function both returns a value (an integer) and produces a side effect (consuming one integer from standard input).
Type checking
In mathematics, the definition of a function specifies both the domain and the range. For example, for the harmonic numbers, the domain is the positive integers and the range is the positive real numbers. In Python, we do not specify the types of the parameter variables or the type of the return value. As long as Python can apply all of the operations within a function, Python executes the function and returns a value.
If Python cannot apply an operation to a given object because it is of the wrong type, it raises a run-time error to indicate the invalid type. For example, if you call the square() function defined earlier with an int argument, the result is an int; if you call it with a float argument, the result is a float. However, if you call it with a string argument, then Python raises a TypeError at run time.
This flexibility is a popular feature of Python (known as polymorphism) because it allows us to define a single function for use with objects of different types. It can also lead to unexpected errors when we call a function with arguments of unanticipated types. In principle, we could include code to check for such errors, and we could carefully specify which types of data each function is supposed to work with. Like most Python programmers, we refrain from doing so. However, in this book, our message is that you should always be aware of the type of your data, and the functions that we consider in this book are built in line with this philosophy, which admittedly clashes with Python’s tendency toward polymorphism. We will discuss this issue in some detail in SECTION 3.3.
THE TABLE BELOW SUMMARIZES OUR DISCUSSION by collecting together the function definitions that we have examined so far. To check your understanding, take the time to reread these examples carefully.
primality test |
def isPrime(n):
if n < 2: return False
i = 2
while i*i <= n:
if n % i == 0: return False
i += 1
return True |
hypotenuse of a right triangle |
def hypot(a, b)
return math.sqrt(a*a + b*b) |
generalized harmonic number |
def harmonic(n, r=1):
total = 0.0
for i in range(1, n+1):
total += 1.0 / (i ** r)
return total |
draw a triangle |
def drawTriangle(x0, y0, x1, y1, x2, y2):
stddraw.line(x0, y0, x1, y1)
stddraw.line(x1, y1, x2, y2)
stddraw.line(x2, y2, x0, y0) |
Typical code for implementing functions |
|