Histograms in CUDA: Privatized for Fast, Level Performance
- One Global Histogram—and Contention
- Per-Block Histograms
- Privatized (Per Thread) Histograms
- Performance
- Conclusion
- Notes
If you were trying to characterize a set of Mars' M&M candies, one of the more obvious ways to do so would be to examine each candy and record its color. Wikipedia lists eight (8) main colors of M&M over the decades: blue, brown, green, orange, red, tan, violet, and yellow. If you start with eight counters—one for each color—and for each candy increment the counter corresponding to the color of the candy, you will have constructed a histogram, a statistical function that counts the number of observations that fall into each of some number of discrete categories. An often-used metaphor for histograms is to say that each input element is put into a specific bin. The M&M candies would have eight bins, and after processing some set of M&M's, the histogram would be represented by the number of candies in each bin. Histograms are often depicted as graphical representations of the data distribution. For computers, however, a histogram usually consists of an array of k integers, where k is the number of bins; in the case of our M&M candies example, k==8. After accumulating N observations, the sum of the k integers is equal to N.
As an example, I recorded the colors of the 24 M&M's from a snack-size bag:
BOYRGBYRVYOBVBYGRVVBBGGR
With one bucket per possible color, Table 1 gives the counts. Note that this random sample did not contain any tan candies, so the T count is 0.
Table 1
Number of Candies by Color
|
Color |
Number |
|
B (Blue/Brown) |
6 |
|
G (Green) |
4 |
|
O (Orange) |
2 |
|
R (Red) |
4 |
|
T (Tan) |
0 |
|
V (Violet) |
4 |
|
Y (Yellow) |
4 |
If k is much smaller than N, as with our colored candies (that is, the number of possible colors is much smaller than the number of candies), then an array of k integers (one for each of the k categories) is a suitable representation for a histogram.
Histograms have many applications. For statisticians, they help to visualize the central location(s), spread, and shape of the input data. Histograms can be used to compute order statistics such as the median (middle) element. In image processing, the peaks and valleys of the histogram can be used for thresholding for image segmentation.
A final application of histograms that deserves mention is counting sort: If the k bins in the histogram are in sorted order, you can emit a sorted list by sweeping across the histogram bins [0..k–1] and using the count in the histogram bin to emit that number of elements. For our example of 24 candies, we can use the histogram to emit the following array, sorted in order of candy color:
BBBBBBGGGGOORRRRVVVVYYYY
This sort is not done by sorting the array per se, but by simply printing the letter B six times (since the histogram element for B is 6), the letter G four times (since the G histogram element is 4), and so on. If each histogram element can be processed in constant time, counting sort runs in O(N) time. Because it does not compare elements, counting sort is not subject to the minimum asymptotic O(NlgN) runtime of comparison-based sorting algorithms.
Counting sort harkens to an alternative solution for computing the histogram, one that is suitable when N is much smaller than k (for example, if N is the number of transactions by a customer and k is the number of items available from an electronic retailer): Sort the N inputs and look for adjacent duplicates to identify the number of elements that belong in each bin of the (sparse) histogram. (CUDA's Thrust library refers to this operation as "reduce_by_key.")
Histograms of any number of elements can be of interest, but for this article we will focus on the special case of 256 elements, which is important for image processing of 8-bit images. Figure 1 shows coins.pgm, the image used in The CUDA Handbook Chapter 15, "Image Processing: Normalized Correlation."

Figure 1 The coins.pgm image.
Figure 2 shows the histogram for coins.pgm. The histogram has two "spikes" that roughly correspond to the "background" and "coins." An image processing algorithm could "binarize" the image by replacing each pixel with a 0 or 1, depending on whether the pixel value was above or below a threshold selected by analyzing the histogram.
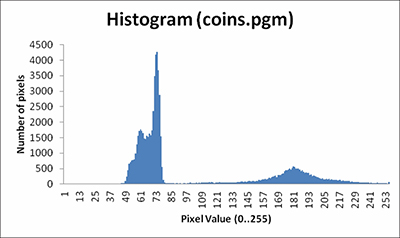
Figure 2 Histogram for coins.pgm.
For this image and histogram, a value around 100 works; Figure 3 shows the resulting black-and-white image.
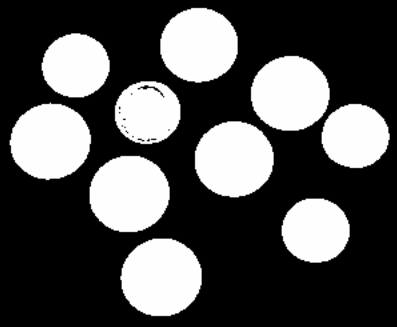
Figure 3 coins.pgm, binarized with a threshold of 100.
For the remainder of this article, we will focus on 256-element histograms of 8-bit input data. For clarity, the code will not use texturing or 2D pitch memory (though such code is included in the sample code on GitHub). Listing 1 gives the C code to compute a histogram: The output array is initialized to zero; then, for each input element, the corresponding histogram element is incremented.
Listing 1—1D histogram (CPU implementation).
void
hist1DCPU(
unsigned int *pHist,
unsigned char *p, size_t N )
{
memset( pHist, 0, 256*sizeof(unsigned int) );
for ( size_t i = 0; i < N; i++ ) {
pHist[ p[i] ] += 1;
}
}
Two basic strategies can be used to parallelize the histogram computation:
- Multiple threads update a histogram concurrently.
- Compute multiple histograms and then merge them together into the final output.
On CPUs, the OS and hardware support for multithreading make the first approach prohibitively expensive, whether acquiring and releasing an OS mutex per histogram element or invoking atomic operations via intrinsics such as InterlockedAdd() or sync_add_and_fetch(). In contrast, option 2 can be implemented with a simple fork/join idiom that divides the problem size evenly among threads (say, 1–2 threads per CPU core), and then computes the final output after waiting on the child threads. [1]
One Global Histogram—and Contention
For CUDA, the tradeoffs are more complex, since the hardware supports more threads and provides mechanisms for enforcing mutual exclusion in both global and shared memory. Listing 2 gives a CUDA C implementation that looks similar to the serial CPU implementation of Listing 1; it uses global memory atomics to operate directly on the output histogram. [2]
Listing 2—1D histogram (CUDA implementation).
__global__ void
histogram1DPerGrid(
unsigned int *pHist,
const unsigned char *base, size_t N )
{
for ( size_t i = blockIdx.x*blockDim.x+threadIdx.x;
i < N;
i += blockDim.x*gridDim.x ) {
atomicAdd( &pHist[ base[i] ], 1 );
}
}
Global memory atomics were introduced in SM 1.1, but they were so slow as to be almost unusable. For randomly distributed data, this kernel on flagship chips for Tesla (GeForce GTX 280), Fermi (Tesla M2050), and Kepler (GeForce GRID K520) yields the performance results summarized in Table 2.
Table 2
Global Atomics Performance, SM 1.0 through SM 3.0
|
Chip |
Speed (Mpix/s) |
|
Tesla (GeForce GTX 280) |
58 |
|
Fermi (M2050) |
1530 |
|
Kepler (GeForce GTX 680) |
10720 |
You read that correctly: SM 2.0 increased performance by 26x over SM 1.3, and SM 3.0 increased performance again by another 7x. [3] Apparently NVIDIA thinks developers want fast atomics! (And NVIDIA would be correct.)
One downside of this histogram implementation is data-dependent behavior: If all the input values are the same, the kernel of Listing 2 performs N atomic adds on the same 32-bit memory location. In this case, the hardware facilities that ensure mutual exclusion for atomics suffer from contention. Our test program can measure the effects of contention by reducing the number of possible random values (specified by the --random parameter to the test program).
With threads contending for the hardware facilities that enable atomicity in global memory, performance degrades as the number of possible values goes down, as shown in Table 3.
Table 3
Performance Versus Number of Values
|
Values |
Tesla |
Fermi |
Kepler |
|
256 |
58 |
1530 |
10720 |
|
128 |
39 |
969 |
7074 |
|
64 |
28 |
660 |
4734 |
|
32 |
26 |
749 |
3058 |
|
16 |
22 |
557 |
3767 |
|
8 |
16 |
349 |
4422 |
|
4 |
11 |
210 |
2864 |
|
2 |
7 |
121 |
1725 |
|
1 |
4 |
68 |
988 |
The slowdown in the degenerate case (only a single value in the input image) is 14.5x for Tesla, 22.5x for Fermi, and 11x for Kepler. Most applications cannot tolerate a large performance degradation due solely to the contents of the input data, but data-dependent performance is difficult to avoid in light of the realities of hardware implementation. To achieve so-called "level" performance (which is not data-dependent), software must cope with the hardware limitations.
Loop Unrolling
The CUDA kernel of Listing 2 uses 8-bit loads from global memory, which are much slower than 32- or 64-bit loads due to a lack of coalescing. Coalescing constraints are discussed in detail in The CUDA Handbook Chapter 5, "Memory," but for this article we will simply use 32-bit loads and process four 8-bit values in each loop iteration
The resulting kernel, shown in Listing 3, is more than 20% faster than the kernel of Listing 2.
This combination of loop unrolling and larger memory operands is used throughout the rest of this article; it is even more effective when the operations being unrolled expose more instructions for the compiler to schedule.
Listing 3—1D histogram (unrolled).
__global__ void
histogram1DNaiveAtomic(
unsigned int *pHist,
const unsigned char *base, size_t N )
{
for ( size_t i = blockIdx.x*blockDim.x+threadIdx.x;
i < N/4;
i += blockDim.x*gridDim.x ) {
unsigned int value = ((unsigned int *) base)[i];
atomicAdd( &pHist[ value & 0xff ], 1 ); value >>= 8;
atomicAdd( &pHist[ value & 0xff ], 1 ); value >>= 8;
atomicAdd( &pHist[ value & 0xff ], 1 ); value >>= 8;
atomicAdd( &pHist[ value ] , 1 );
}
}
The performance of Listings 2 and 3 is the same for degenerate input data, as the effects of contention become dominant.