Calculating the Power of the F Test
- Calculating the Cumulative Density Function
- Using Power to Determine Sample Size
This article, the fourth in a four-part series, discusses the relationship of the noncentrality parameter to the F distribution's cumulative density function—and therefore the power of the F test. The concept of statistical power is discussed in the first article in this series, and the statistical power of the t-test is discussed in the second article. The third article discusses the effect of the noncentrality parameter on the F distribution's probability density function.
As you might expect, the noncentrality parameter is used in the formulas for both the F distribution's cumulative density function and its probability density function.
The cumulative density function is the probability that a variable such as the F-ratio will have a value equal to or smaller than the one specified. For example, the cumulative density function for the central F-ratio with 5 and 50 degrees of freedom, at a value of 2.4, is 95%.
In other words, 95% of the observations from a central F distribution with 5 and 50 degrees of freedom have F-ratios of 2.4 and less. You can verify this using Excel's F.DIST() function:
=F.DIST(2.4,5,50,TRUE)
which returns the value 0.95, or FDIST() prior to Excel 2010:
=1-FDIST(2.4,5,50)
Calculating the Cumulative Density Function
The general formula for the F distribution's cumulative density function is lengthy and intimidating, but it can be found in a variety of online sources. Here is how you can go about calculating it in Excel.
You'll need to define five Excel names, which can be either defined constants or (preferably) references to worksheet cells, as follows:
- Lambda: As defined earlier, the ratio of the sum of squares between to the mean square within.
- V_1: The degrees of freedom for the mean square between.
- V_2: The degrees of freedom for the mean square within.
- E: The base of the natural logarithms, 2.7183. You can get this automatically by using Excel's EXP() function: =EXP(1).
- F: The critical value that cuts off the area represented by alpha in the central F distribution. In Figure 1, that value is obtained by =F.INV(1-0.01,V_1,V_2).
Then, array-enter the following formula by first typing it and then holding down Ctrl and Shift as you press Enter:
=1-SUM((((0.5*Lambda)^(ROW(A1:A100)-1))/FACT(ROW(A1:A100)-1))*E^(-Lambda/2)*BETA.DIST((V_1*F)/(V_2+V_1*F),V_1/2+ROW(A1:A100)-1,V_2/2,TRUE))
Figure 1 shows how this all works out on an Excel worksheet. The actual worksheet is part of the workbook that accompanies this article.
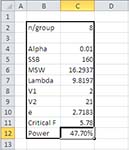
Figure 1 Cells C7:C11 are named according to the text values in cells B7:B11.
The instances of ROW($A$1:$A$101)-1 are there simply to return the numbers 0 through 100 to the formula. Their effect is to divide the area under the curve into 100 slices so that the area in each slice can be quantified and summed.
The formula subtracts that sum from 1 in order to return the area under the noncentral F distribution to the right of the critical F-ratio. That area is the power of the F test.
Using Power to Determine Sample Size
You can use the layout shown in Figure 1 to help determine how large a sample you would need to achieve a particular value for power. The two fundamental reasons that this is a useful check are:
- Too small a sample can prevent you from concluding that a genuine effect exists. Your test's statistical power is too low. It's a waste of resources to run an experiment that's unlikely to enable you to reject a false null hypothesis.
- Too large a sample is another way of wasting resources. Suppose that groups of 35 each result in 90% statistical power. There might be little point to increasing your sample sizes to 70 if doing so would boost power only an additional 2%.
Suppose that you want to boost the power shown in Figure 1 from 47.7% to, say, 90%. There are several ways to do so, including an increase in the strength of the treatments compared to the control groups, and relaxing alpha from 0.01 to, say, 0.05.
But you might not have a feasible way to increase the strength of the treatments, and if you relax alpha you increase statistical power by assuming a greater probability of rejecting a true null hypothesis. There are situations in which doing so is entirely feasible, but you should not be guided solely by considerations of statistical power. Important decisions should be guided by a careful analysis of the long-term costs of making each type of error.