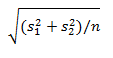The Statistical Power of t-Tests
- Nondirectional Hypotheses
- Making a Directional Hypothesis
- Increasing the Size of the Samples
- The Dependent Groups t-Test
- A Recap
Like this article? We recommend
Like this article? We recommend
Like this article? We recommend
The main intent of this series of four articles is to discuss the meaning and calculation of the statistical power of the F test when used as a criterion for the analysis of variance (ANOVA).
You are reading the second in a series of four articles that discuss statistical power, and how to quantify and visualize it using Microsoft Excel. I suggest that you read The Concept of Statistical Power first. If you wish, continue with the present article, then The Noncentrality Parameter in the F Distribution and Calculating the Power of the F Test.
The present article focuses exclusively on the statistical power of the t-test. The reason is that it is much more straightforward to calculate, and to visualize, the statistical power of the t-test with different designs than to do so with the F-test. Therefore, this article serves as an introduction to the calculation of the power of the F-test.
As the first article in this series noted, the power of a statistical test is the probability that you will reject the null hypothesis when in fact the null hypothesis is false.
A t-test is often used to compare the difference between two means that are based on samples. The samples come from populations. In that context, the test's statistical power is the probability that you will conclude that the two population means are different when they are different. (It can also represent the probability of correctly deciding that one population mean is not just different from but larger than the other.)
Within that context, several different situations can affect the power of the t-test:
- The alternative hypothesis is nondirectional.
- The alternative hypothesis is directional.
- The number of observations changes.
- The design calls for a dependent groups (or "paired") t-test.
The next four sections of this article show the effect of these four situations on the power of the t-test. The effects on the power of the F test are analogous.
Nondirectional Hypotheses
When you make a nondirectional alternative hypothesis to guide your t-test, you state that the population means of the two groups are different. You do not specify which mean you expect to be greater than the other.
The effect of using a nondirectional hypothesis is to divide the alpha—the probability of rejecting a true null hypothesis—between the two tails of the t distribution.
Figure 1 depicts a situation in which the experimenter makes a nondirectional hypothesis.
)
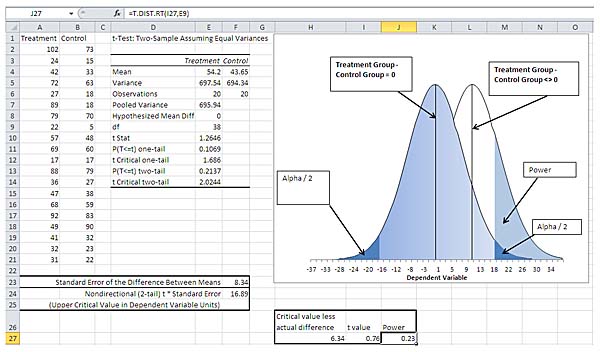
Figure 1 The alpha level is split between the two tails of the curve on the left.
Figure 1 depicts the result of using Excel's Data Analysis add-in to test the difference between the two group means, with the underlying data in cells A2:B21. Notice that I chose the add-in's "equal variances" t-test tool.
The curve on the left in Figure 1 represents the null hypothesis of no difference in the population means. If those two means are equal, then repeated samples that subtract the control mean from the treatment mean will have a long-term average of zero. Some sample differences will be less than zero and some will be greater than zero, and if you charted those differences, you would eventually wind up with a curve that looks like the one on the left in Figure 1.
Paying Off to Alpha
If we set alpha to 5%, we can identify two wedges under the curve, each of which constitutes 2.5% of the area under the curve. Those wedges are identified as "Alpha / 2" in Figure 1.
In fact, we intend to carry out one experiment only. Suppose that the null hypothesis is true. Then we might be unlucky and happen to get for our samples two groups whose mean difference is unusually large: more than 18, say, or less than -17. If we're unlucky, we'll pay off. Based on the unusually large difference between the sample means, we'll conclude that there's a difference in the population means when in fact there isn't.
Getting It Right When There's a Difference
Figure 1 also shows a curve, on the right, which represents an alternative reality in which the population treatment mean is different from the population control mean. In this reality, the treatment mean is 10.55 points greater than the control mean, and so the distribution of the differences between sample means has an average of 10.55. Some (hypothetical) samples would have a difference in means greater than 10.55, and some would have a difference smaller than 10.55.
Our selection of an alpha level causes us to accept the null hypothesis—and to reject the alternative hypothesis—if we get a sample mean difference that’s between -17 and 18. Those critical values are the ones that cut off the two wedges in the curve on the left.
But if we get a mean difference greater than 18 or less than -17, we'll reject the null hypothesis. If the reality of the situation is that the population mean difference is not zero, then we will have gotten it right: We'll reject the null when it's false.
If the population difference is actually 10.55, then we can quantify the power of the t-test in this situation. It is the area under the right-hand curve that's to the right of the critical value. It is the probability that—assuming the alternative hypothesis is true—we will get a sample result that is larger than our critical value. It is the power of the t-test.
Quantifying the Power
In Excel, we can quantify that power, as follows.
Take the difference between the critical value (16.89, shown in Figure 1, cell F24) and the mean of the right-hand curve (10.55, the difference between the treatment mean and the control mean in cells E4:F4). That difference is 6.34.
Divide 6.34 by the standard error of the difference between the means. The standard error in this case is 8.34, shown in cell F23 of Figure 1. The result of the division is 0.76, and it is a t value: the difference between a mean and a criterion, divided by its standard error.
NOTE
When both groups have the same number of observations, one formula for the standard error is as follows:
Use Excel's T.DIST.RT() function to return the proportion of the area under a t distribution to the right of a t value of 0.76 with 38 degrees of freedom:
T.DIST.RT(.76,38) = 0.23
In words, the power of this t-test is 0.23 or 23%. That's not a very powerful test. The next three sections of this article discuss how to increase the test's power.