The C++ Standard Library: Utilities
- 5.6. Compile-Time Fractional Arithmetic with Class ratio<>
- 5.7. Clocks and Timers
5.6. Compile-Time Fractional Arithmetic with Class ratio<>
Since C++11, the C++ standard library provides an interface to specify compile-time fractions and to perform compile-time arithmetic with them. To quote [N2661:Chrono] (with minor modifications):26
- The ratio utility is a general purpose utility inspired by Walter E. Brown allowing one to easily and safely compute rational values at compile time. The ratio class catches all errors (such as divide by zero and overflow) at compile time. It is used in the duration and time_point libraries [see Section 5.7, page 143] to efficiently create units of time. It can also be used in other “quantity” libraries (both standard-defined and user-defined), or anywhere there is a rational constant which is known at compile time. The use of this utility can greatly reduce the chances of runtime overflow because a ratio and any ratios resulting from ratio arithmetic are always reduced to lowest terms.
The ratio utility is provided in <ratio>, with class ratio<> defined as follows:
namespace std {
template <intmax_t N, intmax_t D = 1>
class ratio {
public:
typedef ratio<num,den> type;
static constexpr intmax_t num;
static constexpr intmax_t den;
};
}
intmax_t designates a signed integer type capable of representing any value of any signed integer type. It is defined in <cstdint> or <stdint.h> with at least 64 bits. Numerator and denominator are both public and are automatically reduced to the lowest terms. For example:
// util/ratio1.cpp
#include <ratio>
#include <iostream>
using namespace std;
int main()
{
typedef ratio<5,3> FiveThirds;
cout << FiveThirds::num << "/" << FiveThirds::den << endl;
typedef ratio<25,15> AlsoFiveThirds;
cout << AlsoFiveThirds::num << "/" << AlsoFiveThirds::den << endl;
ratio<42,42> one;
cout << one.num << "/" << one.den << endl;
ratio<0> zero;
cout << zero.num << "/" << zero.den << endl;
typedef ratio<7,-3> Neg;
cout << Neg::num << "/" << Neg::den << endl;
}
The program has the following output:
5/3 5/3 1/1 0/1 -7/3
Table 5.19 lists the compile-time operations defined for ratio types. The four basic arithmetic compile-time operations +, -, *, and / are defined as ratio_add, ratio_subtract, ratio_multiply, and ratio_divide. The resulting type is a ratio<>, so the static member type yields the corresponding type. For example, the following expression yields std::ratio<13,21> (computed as 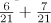 ):
):
std::ratio_add<std::ratio<2,7>,std::ratio<2,6>>::type
Table 5.19. Operations of ratio<> Types
|
Operation |
Meaning |
Result |
|
ratio_add |
Reduced sum of ratios |
ratio<> |
|
ratio_add |
Reduced difference of ratio |
ratio<> |
|
ratio_multiply |
Reduced product of ratios |
ratio<> |
|
ratio_divide |
Reduced quotient of ratios |
ratio<> |
|
ratio_equal |
Checks for!== |
true_type or false_type |
|
ratio_not_equal |
Checks for != |
true_type or false_type |
|
ratio_less |
Checks for < |
true_type or false_type |
|
ratio_less_equal |
Checks for <= |
true_type or false_type |
|
ratio_greater |
Checks for > |
true_type or false_type |
|
ratio_greater_equal |
Checks for >= |
true_type or false_type |
In addition, you can compare two ratio types with ratio_equal, ratio_not_equal, ratio_less, ratio_less_equal, ratio_greater, or ratio_greater_equal. As with type traits, the resulting type is derived from true_type or false_type (see Section 5.4.2, page 125), so its member value yields true or false:
ratio_equal<ratio<5,3>,ratio<25,15>>::value// yields true
As written, class ratio catches all errors, such as divide by zero and overflow, at compile time. For example,
ratio_multiply<ratio<1,numeric_limits<long long>::max()>,
ratio<1,2>>::type
won’t compile, because 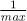 times
times 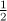 results in an overflow, with the resulting value of the denominator exceeding the limit of its type.
results in an overflow, with the resulting value of the denominator exceeding the limit of its type.
Similarly, the following expression won’t compile, because this is a division by zero:
ratio_divide<fiveThirds,zero>::type
Note, however, that the following expression will compile because the invalid value is detected when member type, num, or den are evaluated:
ratio_divide<fiveThirds,zero>
Predefined ratios make it more convenient to specify large or very small numbers (see Table 5.20). They allow you to specify large numbers without the inconvenient and error-prone listing of zeros. For example,
std::nano
is equivalent to
std::ratio<1,1000000000LL>
which makes it more convenient to specify, for example, nanoseconds (see Section 5.7.2, page 145). The units marked as “optional” are defined only if they are representable by intmax_t.
Table 5.20. Predefined ratio Units
| Name |
Unit |
|
yocto |
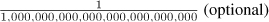
|
|
zepto |
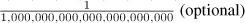
|
|
atto |
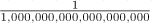
|
|
femto |
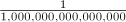
|
|
pico |
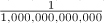
|
|
nano |
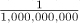
|
|
micro |
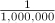
|
|
milli |
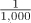
|
|
centi |
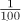
|
|
deci |
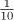
|
|
deca |
10 |
|
hecto |
100 |
|
kilo |
1, 000 |
|
mega |
1, 000, 000 |
|
giga |
1, 000, 000, 000 |
|
tera |
1, 000, 000, 000, 000 |
|
peta |
1, 000, 000, 000, 000, 000 |
|
exa |
1, 000, 000, 000, 000, 000, 000 |
|
zetta |
1, 000, 000, 000, 000, 000, 000, 000 (optional) |
|
yotta |
1, 000, 000, 000, 000, 000, 000, 000, 000 (optional) |