Choosing the Right Algorithm in C++
In the 2011 movie “Battle for the Planet of the Apes,” the ape that is best at solving problems ends up ruling the world. In the business of computers, the programmer who can best devise ways to solve problems ends up maybe not running the world but (hopefully) at least gets good stock options.
An algorithm is a systematic method for solving problems—a recipe, if you will. The word itself is derived from the name of the Arab who invented algebra and was one of the greatest mathematicians of all time. There are several aspects to good algorithms: efficiency, brevity, and correct use of data. This article discusses these by comparing recursive and iterative algorithms.
Recursion Versus Iteration
One of the techniques you may have read about in textbooks is recursion, in which a function calls itself. The technique does not lead to infinite regression if done correctly. One of the simplest examples is the factorial function, denoted in math as n!. For example:
3! = 1 * 2 * 3 5! = 1 * 2 * 3 * 4 * 5
It might seem this is a perfect case in which to use recursion.
int factorial(int n) {
if (n > 1)
return n * factorial(n-1);
else
return 1;
}
Simple, right? If n is 1 or less, return 1, otherwise, multiply n by the factorial of n-1. Mathematically, it's beautiful.
But is it efficient? In these days of super-fast CPUs and cheap memory, it might seem you don't need to be concerned about efficiency. But that’s not true. A solution is not automatically better because it involves fewer lines of code; in fact, there is often a trade-off between saving space (in the size of the function definition) and reducing execution time.
Later in this article, I’ll introduce you to an algorithm that is breath-taking in terms of its brevity—but it can cause the computer to take hours to respond rather than milliseconds. So never ignore efficiency altogether. How is the program using its resources? Is it calculating and storing information in a redundant way or doing just the calculations it needs to?
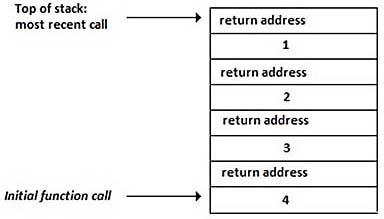
The recursive factorial program puts unnecessary data on the stack—not just any stack but the stack, the area of memory set aside for the purpose of function calls and parameters. When you call factorial(4), the resulting stack is:
Each function call causes the return address and the current value of the argument, n, to be placed onto the stack. (Alternatively, you can imagine this process in the reverse order and think of the stack as growing downward, as long as you are consistent.)
As the function calls return, the argument is multiplied by the return value, and that product accumulates as the program pops down through the stack. Now consider an iterative solution. (“Iteration” just means repetition.)
int factorial(int n) {
int product = 1;
for (int i = 1; i <= n; i++)
product *= i;
return product;
}
This version lacks the elegance of the recursive version, but it involves no unnecessary function-call overhead. Two variables within a single function call are sufficient. This approach stores only the information it needs to—the current values of product and i: