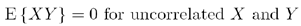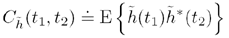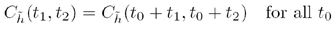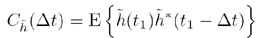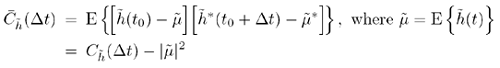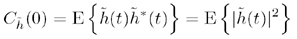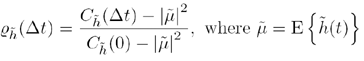Wireless Communications: Modeling Random Fading Channels
- Channel Correlation
- Power Spectral Density (PSD)
- Joint Statistics
- Width of the PSD
- Chapter Summary
- Problems
Groves of trees rustling in the wind scramble received power from one second to the next in a point-to-point microwave link. Or a cellular handset drops a call after moving just a few centimeters from an operable location. Or the tap-delay line filter of a linear equalizer becomes unstable, incapable of canceling the intersymbol interference experienced by a wireless receiver. While the causes and effects of each channel-related problem are varied, the channel analysis is nearly identical for each case - if rigorous stochastic channel modeling is employed.
The goal of this chapter is to develop the terminology, definitions, and basic concepts of modeling a random wireless channel that can be a function of time, frequency, and receiver position in space. While the task of joint characterization may seem daunting, only a few basic concepts are required. In fact, this chapter applies the concept of duality to show that understanding random fading in one dependency leads immediately to understanding in others.
The chapter is broken into the following sections:
-
Section 3.1: Concept of correlation in a random channel process.
-
Section 3.2: Definition of a random process power spectral density.
-
Section 3.3: Representation of random channels with multiple dependencies.
-
Section 3.4: Definition of RMS spectral spreads.
-
Section 3.5: Summary of important concepts.
By the conclusion of the chapter, the reader will be familiar with most of the terms and constructs of random process theory used to describe unpredictable space–time wireless channels. A short review of random process basics is also included in Appendix C for reference.
3.1 Channel Correlation
This section introduces the principle of stochastic channel correlation. Autocorrelation functions are then defined for the complex baseband channel in frequency, time, and space.
3.1.1 The Meaning of Correlation
In probability theory, correlation is a measure of conditional predictability, usually made between two observations of a random event. When we compare two random variables, X and Y, we say that X and Y are dependent if an observation of X provides some predictive information about an observation of Y, and vice versa. Correlation is one measure of dependency between random variables. Increased correlation between random events implies increased predictability. We would expect a strong correlation, for example, between random events such as the amount of sunshine and the average temperature of a given day. After all, sunny days are usually warmer than cloudy days.
If X and Y are uncorrelated, then knowing the value of X does not provide predictive information about Y, and vice versa. We would expect no correlation, for example, between random events such as the amount of sunshine and the monetary winnings of a game of poker played on the same day. (Those two events are also likely to be independent as well.) We can define the condition for uncorrelated random variables with more mathematical rigor:
Thus, if the above ensemble average evaluates to 0, we say that X and Y are uncorrelated. Equation (3.1.1) is only valid for zero-mean random variables.
The concept of correlation is also useful for describing the evolution of random
processes - even complex random processes. Consider the time-varying
random process, 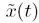 ,
in Figure 3.1, used
here to describe correlation in qualitative terms. While we may not know the
values of each realization of the random process at times t1
and t2, we do know that t1 and t2
are close in time. Thus, we expect that knowing either
,
in Figure 3.1, used
here to describe correlation in qualitative terms. While we may not know the
values of each realization of the random process at times t1
and t2, we do know that t1 and t2
are close in time. Thus, we expect that knowing either 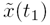 or
or 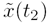 provides a close estimate of the other - they are highly correlated.
Sample values of
provides a close estimate of the other - they are highly correlated.
Sample values of 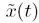 taken at t1 and t3 are farther apart in
time and less correlated. Sample values of
taken at t1 and t3 are farther apart in
time and less correlated. Sample values of 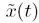 taken at t1 and t4 are very far apart in
time and probably uncorrelated, since knowledge of
taken at t1 and t4 are very far apart in
time and probably uncorrelated, since knowledge of 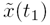 gives virtually no information of
gives virtually no information of 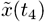 ;
the random process changes a great deal over the interval [t1,
t4]. As a rule of thumb, correlation between samples in a
random process decreases as the time or distance separating them increases,
though the decrease is not always monotonic.
;
the random process changes a great deal over the interval [t1,
t4]. As a rule of thumb, correlation between samples in a
random process decreases as the time or distance separating them increases,
though the decrease is not always monotonic.
 Figure 3.1. Correlation between samples with different separations in a complex random process (sketch of single realization).
Figure 3.1. Correlation between samples with different separations in a complex random process (sketch of single realization).
The relationship between sample correlation and sample separation provides the starting point for characterizing the behavior of random process evolution. This type of analysis is a study in self-correlation or autocorrelation. The next section provides the rigorous definition of random process autocorrelation.
3.1.2 Autocorrelation Relationships
The most common way to characterize the development of a stochastic process
is by calculating the autocorrelation of a function. The definition for an autocorrelation,
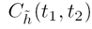 ,
of a time-varying stochastic channel,
,
of a time-varying stochastic channel, 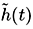 ,
is
,
is
Equation (3.1.2) captures the time-evolution of 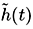 by averaging the products of all samples in the random process ensemble at two
different points in time, t1 and t2. Thus,
by averaging the products of all samples in the random process ensemble at two
different points in time, t1 and t2. Thus,
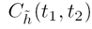 is a snapshot of the typical correlation behavior for a random channel
is a snapshot of the typical correlation behavior for a random channel 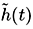 .
.
Most of the stochastic processes studied in this book and in channel modeling theory are wide-sense stationary (WSS). The autocorrelation of a WSS stochastic process, by definition, depends only on the difference in time between t1 and t2. In other words, the correlation behavior is invariant of absolute time:
Therefore, a WSS autocorrelation is usually written as the function of one time variable, Δt, which is equal to the difference, t1 – t2. This WSS definition for autocorrelation is shown below:
Similar WSS autocorrelation definitions exist for stochastic channels that are functions of frequency, f, and space, r.
There is a second condition that must hold for a stochastic process to be truly
WSS. In addition to being autocorrelation stationary, a stochastic process
must also be mean stationary. Using the time-varying baseband channel
as an example, mean stationarity holds if the value E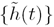 is not a function of time, t. Most processes encountered in real-life
modeling fail the WSS test due to their autocorrelation statistics. Be aware,
however, that certain processes exist having nonstationary means and
stationary autocorrelations.
is not a function of time, t. Most processes encountered in real-life
modeling fail the WSS test due to their autocorrelation statistics. Be aware,
however, that certain processes exist having nonstationary means and
stationary autocorrelations.
An autocorrelation function is considered a second-order statistic because it characterizes behavior between two samples within the random process. The term order refers to the number of samples involved in the computation of the statistic. Here are some example statistics:
3.1.3 Autocovariance
There are several useful variations on the definition of an autocorrelation
function. First, if the process is a zero-mean process, then the autocorrelation
is said to be an autocovariance. Using the time-varying channel as an
example, if E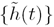 = 0, then the function
= 0, then the function 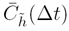 is an autocovariance function. Otherwise, the following definition for autocovariance,
is an autocovariance function. Otherwise, the following definition for autocovariance,
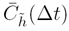 ,
may be used, which removes the mean value,
,
may be used, which removes the mean value, 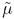 ,
of the WSS process:
,
of the WSS process:
For many autocorrelation functions of the complex baseband channel, 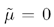 and the autocorrelation is an autocovariance. The definition in Equation
(3.1.5) is most useful when studying random processes of envelope and power,
which have a positive mean value.
and the autocorrelation is an autocovariance. The definition in Equation
(3.1.5) is most useful when studying random processes of envelope and power,
which have a positive mean value.
3.1.4 Unit Autocovariance
A second useful definition, the unit autocovariance, is an autocovariance function that has been normalized against the mean power of the process. In terms of the time-varying stochastic channel, mean power is equal to the autocorrelation evaluated at Δt = 0:
Thus, the full definition for a unit autocovariance, hereafter denoted 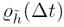 ,
is given in terms of the autocorrelation by
,
is given in terms of the autocorrelation by
The normalization of the unit autocovariance makes it the most convenient,
dimensionless measure of correlation within a random process. It can be shown
that 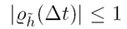 for all values of Δt. A unit autocovariance of 1 indicates perfect
correlation, while a value of 0 indicates the absence of correlation - regardless
of the magnitude of
for all values of Δt. A unit autocovariance of 1 indicates perfect
correlation, while a value of 0 indicates the absence of correlation - regardless
of the magnitude of 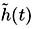 .
.
The definition of unit autocovariance will arise in the study of random envelope processes; most formalized definitions of channel coherence are based on the unit autocovariance of received voltage envelope.