One-Degree of Freedom Internal Model Control
- Introduction
- Properties of IMC
- IMC Designs for No Disturbance Lag
- Design for Processes with No Zeros Near the Imaginary Axis or in the Right Half of the s-Plane
- Design for Processes with Zeros Near the Imaginary Axis
- Design for Processes with Right Half Plane Zeros
- Problems with Mathematically Optimal Controllers
- Modifying the Process to Improve Control System Performance
- Software Tools for IMC Design
- Summary
- Problems
- References
Objectives of the Chapter
-
Present the one-degree of freedom (1DF) Internal Model Control (IMC) structure and describe its properties.
-
Provide design methods for 1DF IMC systems with perfect models that give the best possible performance consistent with noisy measurements for inherently stable processes.
Prerequisite Reading
Chapter 2,"Continuous-Time Models"
Appendix A, "Review of Basic Concepts"
Appendix B, "Frequency Response Analysis"
3.1 Introduction
This chapter introduces methods for designing feedback controllers to force the output of an inherently stable process to (1) respond in a desired manner to a setpoint change, and (2) counter the effects of disturbances that enter directly into the process output. To enable us to carry out a quantitative controller design, we assume that we have a mathematical model of the process that allows us to predict how the process output (sometimes also called the process variable) responds to the control effort (e.g., how a process flow responds to the opening or closing of a valve) and to disturbances. Further, to keep these initial discussions as simple as possible, we assume that (1) the mathematical model is a perfect representation of the process, (2) the process is linear, and (3) there are no constraints on the control effort so it can take on any value between plus and minus infinity. Chapter 7 extends the results of this chapter to the case of imperfect models and uncertain processes. Chapter 5 shows how the controller designs obtained in this chapter and Chapter 4 can be implemented so as to accommodate control effort saturation. Chapter 6 shows how the IMC designs of this and the next chapter can be converted into PID controllers. While the treatment of nonlinear process models is beyond the scope of this text, many of the controller design concepts for linear models carry over to fairly broad classes of nonlinear process models (see, for example, Kravaris, 1987).
The IMC structure (Garcia & Morari, 1982) given in Figure
3.1 is central to our discussions on the design of controllers. Its conceptual
usefulness lies in the fact that it allows us to concentrate on the controller
design without having to be concerned with control system stability provided
that the process model 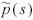 is a perfect representation of a stable process p(s).
is a perfect representation of a stable process p(s).
 Figure 3.1. The IMC system.
Figure 3.1. The IMC system.
As we shall see in Chapter 7, even if the model is imperfect, it is still possible to design the controller q(s, 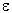 ) without concern for system stability, and then select the tuning parameter
) without concern for system stability, and then select the tuning parameter 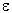 in q(s,
in q(s, 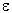 ) to assure stability, provided only that the process p(s) is inherently stable. In addition, if the controller gain is the inverse of the model gain, then the process output y(s) will eventually reach and maintain the setpoint r (in the absence of new disturbances), provided only that the process and model gains have the same sign and that the controller
is tuned so as to assure stability. For these reasons, the structure of Figure 3.1 is well suited for exploring ideal control system performance. Further, since the structure of Figure 3.1 can be rearranged into other structures, it can be used to obtain the controller for these other structures. We shall show
how this is done for classical PID feedback control in Chapter 6.
) to assure stability, provided only that the process p(s) is inherently stable. In addition, if the controller gain is the inverse of the model gain, then the process output y(s) will eventually reach and maintain the setpoint r (in the absence of new disturbances), provided only that the process and model gains have the same sign and that the controller
is tuned so as to assure stability. For these reasons, the structure of Figure 3.1 is well suited for exploring ideal control system performance. Further, since the structure of Figure 3.1 can be rearranged into other structures, it can be used to obtain the controller for these other structures. We shall show
how this is done for classical PID feedback control in Chapter 6.
While investigators have made use of concepts similar to those of IMC to design optimal feedback controllers since the late
1950s (Newton, Gould, & Kaiser, 1957), it was not until 1974 that the German investigator Frank first proposed utilizing the
structure shown in Figure 3.1 to control processes. In 1979, Brosilow recognized that the IMC structure was at the core of both his inferential control
system (Brosilow, 1979; Joseph & Brosilow, 1978a, 1978b; Tong & Brosilow, 1978) and the Smith Predictor (Smith, 1957), and
proposed methods for designing the controller q(s, 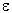 ). Morari and his coworkers, in a series of papers (Garcia & Morari, 1982, 1985a, 1985b; Morari, 1983, 1985; Morari, Skogestad,
& Rivera 1984; Morari & Zafiriou, 1989), greatly expanded on the design methods for q(s,
). Morari and his coworkers, in a series of papers (Garcia & Morari, 1982, 1985a, 1985b; Morari, 1983, 1985; Morari, Skogestad,
& Rivera 1984; Morari & Zafiriou, 1989), greatly expanded on the design methods for q(s, 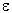 ) and placed the methodology in a sound theoretical framework. During this period, it also became clear that the IMC structure
underlies the industrially important model predictive controllers known as IDCOM (Richalet, 1978), DMC (Cutler & Ramaker,
1979), and QDMC (Garcia & Morshedi, 1986; Prett & Garcia, 1988).
) and placed the methodology in a sound theoretical framework. During this period, it also became clear that the IMC structure
underlies the industrially important model predictive controllers known as IDCOM (Richalet, 1978), DMC (Cutler & Ramaker,
1979), and QDMC (Garcia & Morshedi, 1986; Prett & Garcia, 1988).