Basic Rendering in OpenGL
- The Basic Graphics Pipeline
- Setting Up Your Coordinate System
- Using the Stock Shaders
- Connecting The Dots
- Blending
- Summary
by Richard S. Wright, Jr.
What You'll Learn in This Chapter
- About the basic OpenGL rendering architecture
- How to use the seven OpenGL geometric primitives
- How to use stock shaders
- How to use uniforms and attributes
- How to submit geometry with the GLBatch helper class
- How to perform depth testing and back face culling
- How to draw transparent or blended geometry
- How to draw antialiased points, lines, and polygons
If you've ever had a chemistry class (and probably even if you haven't), you know that all matter consists of atoms and all atoms consist of only three things: protons, neutrons, and electrons. All the materials and substances you have ever come into contact with—from the petals of a rose to the sand on the beach—are just different arrangements of these three fundamental building blocks. Although this explanation is a little oversimplified for almost anyone beyond the third or fourth grade, it demonstrates a powerful principle: With just a few simple building blocks, you can create highly complex and beautiful structures.
The connection is fairly obvious. Objects and scenes that you create with OpenGL also consist of smaller, simpler shapes, arranged and combined in various and unique ways. This chapter explores these building blocks of 3D objects, called primitives, and the various ways you can combine them on-screen. All primitives in OpenGL are one-, two-, or three-dimensional objects, ranging from single points to lines and groups of triangles. In this chapter, you learn everything you need to know to draw objects in three dimensions from these simpler shapes.
The Basic Graphics Pipeline
A primitive in OpenGL is simply a collection of vertices, hooked together in a predefined way. A single point for example is a primitive that requires exactly one vertex. Another example is a triangle, a primitive made up of three vertices. Before we talk about the different kinds of primitives, let's take a look first at how a primitive is assembled out of individual vertices. The basic rendering pipeline takes three vertices and turns them into a triangle. It may also apply color, one or more textures, and move them about. This pipeline is also programmable; you actually write two programs that are executed by the graphics hardware to process the vertex data and fill in the pixels (we call them fragments because actually there can be more than one fragment per pixel, but more on that later) on-screen. To understand how this basic process works in OpenGL, let's take a look at a simplified version of the OpenGL rendering pipeline, shown here in Figure 3.1.
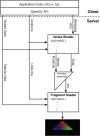
Figure 3.1 How to render a triangle.
Client-Server
First notice that we have divided the pipeline in half. On the top is the client side, and on the bottom is the server. Basic client-server design is applied when the client side of the pipeline is separated from the server side functionally. In OpenGL's case, the client side is code that lives in the main CPU's memory and is executed within the application program, or within the driver in main system memory. The driver assembles rendering commands and data and sends to the server for execution. On a typical desktop computer, the server is across some system bus and is in fact the hardware and memory on the graphics card.
Client and server also function asynchronously, meaning they are both independent pieces of software or hardware, or both. To achieve maximum performance, you want both sides to be busy as much as possible. The client is continually assembling blocks of data and commands into buffers that are then sent to the server for execution. The server then executes those buffers, while at the same time the client is getting ready to send the next bit of data or information for rendering. If the server ever runs out of work while waiting on the client, or if the client has to stop and wait for the server to become ready for more commands or data, we call this a pipeline stall. Pipeline stalls are the bane of performance programmers, and we really don't want CPUs or GPUs standing around idle waiting for work to do.
Shaders
The two biggest boxes in Figure 3.1 are for the vertex shader and the fragment shader. A shader is a program written in GLSL (we get into GLSL programming in Chapter 6, "Thinking Outside the Box: Nonstock Shaders"). GLSL looks a whole lot like C; in fact these programs even start with the familiar main function. These shaders must be compiled and linked together (again much like a C or C++ program) from source code before they can be used. The final ready-to-use shader program is then made up of the vertex shader as the first stage of processing and the fragment shader as the second stage of processing. Note that we are taking a simplified approach here. There is actually something called a geometry shader that can (optionally) fit between here, as well as all sorts of feedback mechanisms for moving data back and forth. There are also some post fragment processing features such as blending, stencil, and depth testing, which we also cover later.
The vertex shader processes incoming data from the client, applying transformations, or doing other types of math to calculate lighting effects, displacement, color values, and so on. To render a triangle with three vertices, the vertex shader is executed three times, once for each vertex. On today's hardware, there are multiple execution units running simultaneously, which means all three vertices are processed simultaneously. Graphics processors today are massively parallel computers. Don't be fooled by clock speed when comparing them to CPUs. They are orders of magnitude faster at graphics operations.
Three vertices are now ready to be rasterized. The primitive assembly box in Figure 3.1 is meant to show that the three vertices are then put together and the triangle is rasterized, fragment by fragment. Each fragment is filled in by executing the fragment shader, which outputs the final color value you will see on-screen. Again, today's hardware is massively parallel, and it is quite possible a hundred or more of these fragment programs could be executing simultaneously.
Of course to get anything to happen, you must feed these shaders some data. There are three ways in which you the programmer pass data to OpenGL shaders for rendering: attributes, uniforms, and textures.
Attributes
An attribute is a data element that changes per vertex. In fact, the vertex position itself is actually an attribute. Attributes can be floating-point, integer, or boolean data, and attributes are always stored internally as a four component vector, even if you don't use all four components. For example, a vertex position might be stored as an x, a y, and a z value. That would be three out of the four components. Internally, OpenGL makes the fourth component (W if you just have to know) a one. In fact, if you are drawing just in the xy plane (and ignoring z), then the third component will be automatically made a zero, and again the fourth will be made a one. To complete the pattern, if you send down only a single floating-point value as an attribute, the second and third components are zero, while the fourth is still made a one. This default behavior applies to any attribute you set up, not just vertex positions, so be careful when you don't use all four components available to you. Other things you might change per vertex besides the position in space are texture coordinates, color values, and surface normals used for lighting calculations. Attributes, however, can have any meaning you want in the vertex program; you are in control.
Attributes are copied from a pointer to local client memory to a buffer that is stored (most likely) on the graphics hardware. Attributes are only processed by the vertex shader and have no meaning to the fragment shader. Also, to clarify that attributes change per vertex, this does not mean they cannot have duplicate values, only that there is actually one stored value per vertex. Usually, they are different of course, but it is possible you could have a whole array of the same values. This would be very wasteful, however, and if you needed a data element that was the same for all the attributes in a single batch, there is a better way.
Uniforms
A uniform is a single value that is, well, uniform for the entire batch of attributes; that is, it doesn't change. You set the values of uniform variables usually just before you send the command to render a primitive batch. Uniforms can be used for virtually an unlimited number of uses. You could set a single color value that is applied to an entire surface. You could set a time value that you change every time you render to do some type of vertex animation (note the uniform changes once per batch, not once per vertex here). One of the most common uses of uniforms is to set transformation matrices in the vertex shader (this is almost the entire purpose of Chapter 4, "Basic Transformations: A Vector/Matrix Primer").
Like attributes, uniform values can be floating-point, integer, or boolean in nature, but unlike attributes, you can have uniform variables in both the vertex and the fragment shader. Uniforms can be scalar or vector types, and you can have matrix uniforms. Technically, you can also have matrix attributes, where each column of the matrix takes up one of those four component vector slots, but this is not often done. There are even some special uniform setting functions we discuss in Chapter 5, "Basic Texturing," that deal with this.
Texture
A third type of data that you can pass to a shader is texture data. It is a bit early to try and go into much detail about how textures are handled and passed to a shader, but you know from Chapter 1, "Introduction to 3D Graphics and OpenGL," basically what a texture is. Texture values can be sampled and filtered from both the vertex and the fragment shader. Fragment shaders typically sample a texture to apply image data across the surface of a triangle. Texture data, however, is more useful than just to represent images. Most image file formats store color components in unsigned byte values (8 bits per color channel), but you can also have floating-point textures. This means potentially any large block of floating-point data, such as a large lookup table of an expensive function, could be passed to a shader in this way.
Outs
The fourth type of data shown in the diagram in Figure 3.1 are outs. An out variable is declared as an output from one shader stage and declared as an in in the subsequent shader stage. Outs can be passed simply from one stage to the next, or they may be interpolated in various ways. Client code has no access to these internal variables, but rather they are declared in both the vertex and the fragment shader (and possibly the optional geometry shader). The vertex shader assigns a value to the out variable, and the value is constant, or can be interpolated between vertexes as the primitive is rasterized. The fragment shader's corresponding in variable of the same name receives this constant or interpolated value. In Chapter 6, we see how this works in more detail.