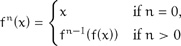Elements of Programming: Transformations and Their Orbits
- 2.1 Transformations
- 2.2 Orbits
- 2.3 Collision Point
- 2.4 Measuring Orbit Sizes
- 2.5 Actions
- 2.6 Conclusions
Also read the PDF version of this chapter and the preface to Elements of Programming.
This chapter defines a transformation as a unary regular function from a type to itself. Successive applications of a transformation starting from an initial value determine an orbit of this value. Depending only on the regularity of the transformation and the finiteness of the orbit, we implement an algorithm for determining orbit structures that can be used in different domains. For example, it could be used to detect a cycle in a linked list or to analyze a pseudorandom number generator. We derive an interface to the algorithm as a set of related procedures and definitions for their arguments and results. This analysis of an orbit-structure algorithm allows us to introduce our approach to programming in the simplest possible setting.
2.1 Transformations
While there are functions from any sequence of types to any type, particular classes of signatures commonly occur. In this book we frequently use two such classes: homogeneous predicates and operations. Homogeneous predicates are of the form T × ... × T → bool; operations are functions of the form T × ... × T → T. While there are n-ary predicates and n-ary operations, we encounter mostly unary and binary homogeneous predicates and unary and binary operations.
A predicate is a functional procedure returning a truth value:
|
Predicate(P) ≜ |
||
|
FunctionalProcedure(P) |
||
|
∧ |
Codomain(P) = bool |
|
A homogeneous predicate is one that is also a homogeneous function:
|
HomogeneousPredicate(P) ≜ |
||
|
Predicate(P) |
||
|
∧ |
HomogeneousFunction(P) |
|
A unary predicate is a predicate taking one parameter:
|
UnaryPredicate(P) ≜ |
||
|
Predicate(P) |
||
|
∧ |
UnaryFunction(P) |
|
An operation is a homogeneous function whose codomain is equal to its domain:
|
Operation(Op) ≜ |
||
|
HomogeneousFunction(Op) |
||
|
∧ |
Codomain(Op) = Domain(Op) |
|
Examples of operations:
int abs(int x) {
if (x < 0) return -x; else return x;
} // unary operation
double euclidean_norm(double x, double y) {
return sqrt(x * x + y * y);
} // binary operation
double euclidean_norm(double x, double y, double z) {
return sqrt(x * x + y * y + z * z);
} // ternary operation
Lemma 2.1.
euclidean_norm(x, y, z) = euclidean_norm(euclidean_norm(x, y), z)
This lemma shows that the ternary version can be obtained from the binary version. For reasons of efficiency, expressiveness, and, possibly, accuracy, the ternary version is part of the computational basis for programs dealing with three-dimensional space.
A procedure is partial if its definition space is a subset of the direct product of the types of its inputs; it is total if its definition space is equal to the direct product. We follow standard mathematical usage, where partial function includes total function. We call partial procedures that are not total nontotal. Implementations of some total functions are nontotal on the computer because of the finiteness of the representation. For example, addition on signed 32-bit integers is nontotal.
A nontotal procedure is accompanied by a precondition specifying its definition space. To verify the correctness of a call of that procedure, we must determine that the arguments satisfy the precondition. Sometimes, a partial procedure is passed as a parameter to an algorithm that needs to determine at runtime the definition space of the procedural parameter. To deal with such cases, we define a definition-space predicate with the same inputs as the procedure; the predicate returns true if and only if the inputs are within the definition space of the procedure. Before a nontotal procedure is called, either its precondition must be satisfied, or the call must be guarded by a call of its definition-space predicate.
Exercise 2.1.
Implement a definition-space predicate for addition on 32-bit signed integers.
This chapter deals with unary operations, which we call transformations:
|
Transformation(F) ≜ |
||
|
Operation(F) |
||
|
∧ |
UnaryFunction(F) |
|
|
∧ |
DistanceType: Transformation → Integer |
|
We discuss DistanceType in the next section.
Transformations are self-composable: f(x), f(f(x)), f(f(f(x))), and so on. The definition space of f(f(x)) is the intersection of the definition space and result space of f. This ability to self-compose, together with the ability to test for equality, allows us to define interesting algorithms.
When f is a transformation, we define its powers as follows:
|
|
To implement an algorithm to compute fn(x), we need to specify the requirement for an integer type. We study various concepts describing integers in Chapter 5. For now we rely on the intuitive understanding of integers. Their models include signed and unsigned integral types, as well as arbitrary-precision integers, with these operations and literals:
|
Specifications |
C++ |
|
|
Sum |
+ |
+ |
|
Difference |
– |
- |
|
Product |
· |
* |
|
Quotient |
/ |
/ |
|
Remainder |
mod |
% |
|
Zero |
0 |
I(0) |
|
One |
1 |
I(1) |
|
Two |
2 |
I(2) |
where I is an integer type.
That leads to the following algorithm:
template<typename F, typename N>
requires(Transformation(F) && Integer(N))
Domain(F) power_unary(Domain(F) x, N n, F f)
{
// Precondition: n ≥ 0 ∧ (∀i ∊ N)0 < i ≤ n ⇛ fn(x) is defined
while (n != N(0)) {
n = n - N(1);
x = f(x);
}
return x;
}