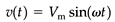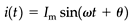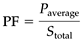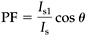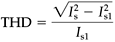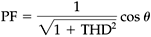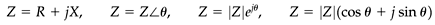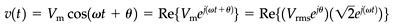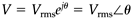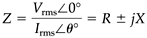Introduction to AC Circuits
- Fundamental Definitions
- AC Circuit Analysis
- Power and Power Triangles in AC Circuits
- Power Factor Correction
- Star-Delta and Delta-Star Conversion in Three-Phase AC Circuits
- Voltage and Currents in Star- and Delta-Connected Loads
- Voltage and Current Phasors in Three-Phase Systems
- Power in Three-Phase AC Circuits
- Three-Phase Power Measurement and Data Logging
- References
Electric power is generated, distributed, and used as sinusoidal voltages and currents in a great variety of commercial and domestic applications. Furthermore, in the industrial world a vast number of small-, medium-, or large-size ac power generators and loads are interlinked. Therefore, the design, operation, maintenance, and management of such systems very much depend on a good understanding of ac circuit theory.
The analysis of ac circuits involves the study of the behavior of the system under both normal and abnormal operating conditions. However, this book is not intended to include abnormal conditions. Instead, it focuses on the foremost fundamental issues and normal conditions and presents visual aids and interactive tools. Additionally, it is assumed that a steady-state sinusoidal condition is reached, which means that all transient effects in ac circuits have disappeared.
This chapter's topics are of practical importance in ac systems. The fundamental terminologies used in ac circuits are introduced, and a number of custom-written VIs, considering both single-phase and three-phase ac circuits, are provided.
The chapter begins with essential definitions of such terms as power factor, phasor, impedance, and per-unit value.
Section 3.2 describes the topological analysis of five basic ac electric circuits containing impedances and ac supplies. Then a reverse study is presented where an unknown impedance is determined by user-defined ac voltage and currents.
Section 3.3 is concerned with a description and visual demonstration of the powers in ac circuits and is followed by a discussion of power factor correction in Section 3.4.
The remaining sections describe various other aspects of three-phase circuits, accompanied by interactive VI modules. The chapter ends with a comprehensive study of real-time three-phase data logging.
Educational Objectives
The chapter develops appropriate relationships and visual aids for describing ac systems using ac voltage, ac current, impedance, ac power, and phasors. After completing this chapter, students should be able to
-
plot and interpret the characteristics of ac voltage, current, and power waveforms.
-
understand the definitions of peak to peak; peak and rms values; and phase/line voltage and current, phase angle, power factor, complex impedance, phasor and base (per-unit) values in ac circuits.
-
state the equations for series, parallel, and combination ac circuits that contain impedances and ac supplies, understand the effects on current caused by changes in impedances, and state the meaning of the term equivalent impedance.
-
analyze the sinusoidal steady-state behavior of single- and three-phase ac circuits using phasors, and study the effect of resistive, inductive, and capacitive loads in single-phase ac circuits.
-
understand the concept of complex power, power measurement methods, and power factor correction.
-
recognize the data logging techniques associated with ac circuits.
3.1 Fundamental Definitions
Steady-state sinusoidal time-varying voltage and current waveforms can be given by
where v and i are the time-varying voltage and current, and Vm and Im are the peak values (magnitudes or amplitudes) of the voltage and current waveforms. In equation 3.2, θ is known as the phase angle, which is normally defined with reference to the voltage waveform.
The term cos θ is called a power factor. Remember that we assumed a voltage having a zero phase. In general, the phase of the voltage may have a value other than zero. Then θ should be taken as the phase of the voltage minus the phase of the current.
In a linear circuit excited by sinusoidal sources, in the steady-state, all voltages and currents are sinusoidal and have the same frequency. However, there may be a phase difference between the voltage and current depending on the type of load used.
The three basic passive circuit elements, the resistor (R), the inductor (L), and the capacitor (C), are considered in this chapter. An ac load may be a combination of these passive elements, such as R + L or R + C.
Note that the current and voltage waveforms in the resistor are in phase, while inductances and capacitors both have a 90° phase shift between voltage and current. The inductor current waveform lags the inductor voltage waveform by 90°, while in the capacitor, the current leads the voltage by 90°.
The peak-to-peak value is also used in the analysis of ac circuits; it is the difference between the highest and lowest values of the waveform over one cycle. This can easily be visualized in the ac waveforms generated.
It might seem difficult to describe an ac signal in terms of a specific value, since an ac signal is not constant. However, as shown in Chapter 2, these sinusoidal signals are periodic, repeating the same pattern of values in each period. Therefore, when a voltage or a current is described simply as ac, we will refer to its rms or effective value, not its maximum value, which simplifies the description of ac signal.
Power Factor
In general, for nonsinusoidal systems (distorted waveforms), the power factor PF is equal to
where Stotal is the total apparent (or complex) power in VA, which is equal to Vrms · Irms.
If the voltage and current waveforms of an ac system are measured in real time, it is much easier to calculate the power factor simply by using the definitions of average and rms values (given in equations 2.3 and 2.4).
However, in many utility applications, the distortion in ac voltage is usually small, hence the voltage waveform can be assumed as an ideal sine wave at fundamental frequency. This assumption simplifies the analysis, which results in an analytical solution of power factor for the nonsinusoidal systems as
where Is is the rms value of the current (as in equation 2.4 for sinusoidal quantities), Is1 is the rms Fourier fundamental component of the current, and cos θ is the power factor in linear circuits with sinusoidal voltages and currents.
From equation 3.4, we can conclude that a large distortion in the current waveform will result in a small value of the current ratio, Is1/Is, which means a small value of power factor, even if θ = 0 (a unity power factor, cos θ = 1).
As seen, since the Fourier analysis is involved for the estimation of Is1, a quantity called total harmonic distortion (THD) can be defined in the current, which simplifies the estimation of PF.
Note that the definitions given for the PF will be utilized in the transformer experiment later since the excitation current of transformers is highly distorted.
Phasors
In most ac circuit studies, the frequency is fixed, so this feature is used to simplify the analysis. Sinusoidal steady-state analysis is greatly facilitated if the currents and voltages are represented as vectors in the complex number plane known as phasors. The basic purpose of phasors is to show the rms value (or the magnitude in some cases) and phase angle between two or multiple quantities, such as voltage and current.
The phasors can be defined in many forms, such as rectangular, polar, exponential, or trigonometric:
where R is the real part and X is the imaginary part of the complex number, and |Z| is the absolute value of Z.
To understand the phasors theoretically, let us consider a sinusoidal voltage function. If the rotating term at angular frequency ω is ignored, the phasor function can be given by using the real part of a complex function in polar form.
and the voltage phasor function is
This phasor is visualized as a vector of length Vrms that rotates counterclockwise in the complex plane with an angular velocity of ω. As the vector rotates, its projection on the real axis traces out the voltage as a function of time. In fact, the “phasor” is simply a snapshot of this rotating vector at t = 0 and will be shown in the phasor graphs of the VIs implemented.
In addition, when the periodic voltage, current, and power waveforms are considered, each data point in these waveforms can be represented in the complex plane. This feature is also demonstrated in the chapter's phasor VIs.
Impedance
The impedance Z in ac circuits is defined as the ratio of voltage function to current function. Hence, the impedance is a complex number and can be expressed in the rectangular form as
The real component of the impedance is called the resistance R and the imaginary component is called the reactance X, both of which are in ohms. The reactance is a function of ω in L and C loads, and for an inductive load, X is positive, whereas for a capacitive load, X is negative (Fig. 3-1).
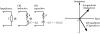 Figure 3-1. Equivalent circuits of an impedance and impedance phasor in the complex plane.
Figure 3-1. Equivalent circuits of an impedance and impedance phasor in the complex plane.
The impedance can also be displayed in the complex plane as phasors, the voltage, and the current waveforms. However, since the resistance is never negative, only the first and fourth quadrants are required. This restriction is implied in the associated VIs by limiting the upper and lower values of the controls.
Per-Unit Values
The per-unit system of measurement and computation is used in electrical engineering for two principal reasons:
-
To display multiple quantities (such as voltages and currents) on the same scale for comparison purposes
-
To eliminate the need for conversion of the voltages, currents, and impedances in the circuits and to avoid using transformation from three-phase to single-phase, and vice versa
The quantity subject to conversion is normalized in terms of a particularly convenient unit, called the per-unit base of the system. Note that whenever per-unit values are given, they are always dimensionless. To calculate the actual values of the quantities, the magnitude of the base of the per-unit system must be known. In electrical circuits, voltage, current, impedance, and power can be selected as base quantities.